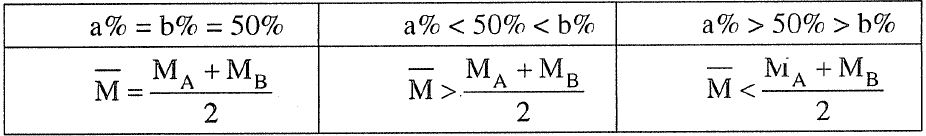I. Lý thuyết
Nội dung của phương pháp này được chia thành nhiều dạng:
- Phương pháp khối lượng mol trung bình (M)
- Phương pháp số nguyên tử cacbon trung bình
- Phương pháp số nguyên tử hiđro trung bình
- Phương pháp gốc hiđrocacbon trung bình
- Phương pháp nhóm chức trung bình
- Phương pháp hóa trị trung bình
Đối với vô cơ thường chỉ sử dụng 2 phương pháp: khối lượng mol trung bình (M) và hóa trị trung bình.
1. Phương pháp khối lượng mol trung bình (M):
* Khái niệm:
Khối lượng mol trung bình (KLMTB) của hỗn hợp là khối lượng của một mol hỗn hợp đó.
Công thức tính KLMTB:
$\overline M = \frac{{{m_{hh}}}}{{{n_{hh}}}} = \frac{{{M_1}{n_1} + {M_2}{n_2} + ... + {M_i}{n_i}}}{{{n_1} + {n_2} + ... + {n_i}}}\left( 1 \right)$
Trong đó :
${m_{hh}}$ là tổng số gam của hỗn hợp.
${n_{hh}}$ là tổng số mol của hỗn hợp.
${M_1},{M_2},{M_i}$ là khối lượng mol của các chất trong hỗn hợp.
${n_1},{n_2},...{n_i}$ là số mol tương ứng của các chất.
* Đối với chất khí vì thể tích tỉ lệ với số mol nên (1) được viết lại:
$\overline M = \frac{{{M_1}{V_1} + {M_2}{V_2} + ... + {M_i}{V_i}}}{{{V_1} + {V_2} + ... + {V_i}}}\left( 2 \right)$
* Với: ${V_1},{V_2},...{V_i}$ lần lượt là thể tích các chất khí tương ứng.
Từ (1) và (2) suy ra:
$\overline M = {M_1}{x_1} + {M_2}{x_2} + ... + {M_i}{x_i}\left( 3 \right)$
Với là thành phần % số mol hoặc thể tích (nếu hỗn hợp khí) tương ứng của các chất và được lấy theo số thập phân ( nghĩa là 100% ứng với X = 1).
Chú ý: Nếu hỗn hợp chỉ có hai chất có khối lượng mol tương ứng $M_1$ và $M_2$ thì các công thức (1), (2), (3) được viết dưới dạng:
(1) suy ra
$\overline M = \frac{{{M_1}{n_1} + {M_2}\left( {n - {n_i}} \right)}}{n}$
(2) suy ra
$\overline M = \frac{{{M_1}{V_1} + {M_2}\left( {V - {V_i}} \right)}}{V}$
(3) suy ra
$\overline M = {M_1}x + {M_2}\left( {1 - x} \right)$
Trong đó ${n_1},{V_1},x$ là số mol, thể tích, thành phần % về số mol hoặc thể tích (hỗn hợp khí) của chất thứ ${M_1}$.
c. Tính chất:
- $\overline M $ không phải là hằng số mà có giá trị phụ thuộc vào thành phần về lượng các chất trong hỗn hợp.
- $\overline M $ luôn nằm trong khoảng khối lượng mol phân tử của chất nhỏ nhất và lớn nhất.
${M_{\min }} < M < {M_{\max }}$
- Hỗn hợp hai chất A, B có có thành phần tính theo số mol tương ứng là a%,b% thì:
2. Vận dụng trong giải toán:
Trong vô cơ, thường gặp các dạng toán xác định khối lượng nguyên tử của 2 kim loại thuộc cùng phân nhóm chính và nằm 2 chu kỳ kế tiếp nhau; xác định thành phần hỗn hợp muối cùng 1 cation hoặc cùng 1 anion; xác định % số lượng mỗi đồng vị 1 nguyên tố; % thể tích các khí trong hỗn hợp.
* Chú ý: Ngoài phương pháp trị số trung bình trên ta còn phương pháp số hạt trung bình
$\sum\nolimits_{hạt} {e + p + n = 2Z + N} $
Với các nguyên tử đồng vị bền ($Z \le 82$) ta luôn có:
$Z \le N \le 1,5Z$
Giả sử trong nguyên tử số hạt $n=p=e=Z.$
$\sum\nolimits_{hạt} { = 3\overline Z \Rightarrow } \overline Z = \sum\nolimits_{hạt} {/3 \Rightarrow Z = } $ phần nguyên của $\overline Z $.
(Chỉ áp dụng cho những nguyên tử có $\sum\nolimits_{hạt} { \le 40} $)
II. Bài tập áp dụng (xem file đính kèm)