1. Đường tiệm cận đứng

Cho hàm số $y = f(x)$ xác định trên một khoảng vô hạn (là khoảng dạng $(a;+∞); (-∞;b)$ hoặc $(-∞;+∞)$ ).

- Định nghĩa: Đường thẳng $x = x_o$ được gọi là đường tiệm cận đứng của đồ thị hàm số nếu ít nhất một trong các điều kiện sau đây được thỏa mãn:

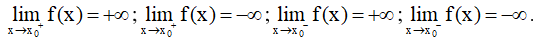
2. Đường tiệm cận ngang

- Định nghĩa: Đường thẳng $y = y_o$ được gọi là đường tiệm cận ngang của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn:

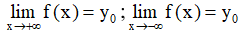
Chú ý:

- Đồ thị hàm số: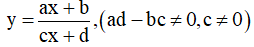 


luôn có tiệm cận ngang và tiệm cận đứng lần lượt là:

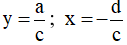
- Nếu 

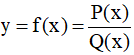
là hàm số phân thức hữu tỉ.

+ Nếu Q(x) = 0 có nghiệm là $x_o$, và $x_o$ không là nghiệm của $P(x) = 0$ thì đồ thị có tiệm cận đứng là $x = x_o$.

+ Nếu bậc (P(x)) ≤ bậc (Q(x)) thì đồ thị hàm số có tiệm cận ngang.Dạng 1. Xác định tiệm cận của hàm số.

II. Dạng bài tập thường gặp 

    1. Xác định tiệm cận của hàm số

Ví dụ:

Câu 1: Cho hàm số: 

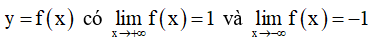
Khẳng định nào sau đây là khẳng định đúng ?

A. Đồ thị hàm số không có tiệm cận ngang.

B. Đồ thị hàm số có đúng một tiệm cận ngang.

C. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng $y = 1$ và $y = -1.$

D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng $x = 1$ và $x = -1.$
(Đáp án: C)

Câu 2: Cho hàm số: 

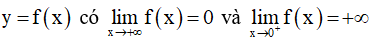
Khẳng định nào sau đây là khẳng định đúng ?

A. Đồ thị hàm số đã cho không có tiệm cận đứng.

B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho.

C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng .

D. Hàm số đã cho có tập xác định là $D = (0,+∞).$
(Đáp án: B)

          2. Tìm $m$ để hàm số có tiệm cận thỏa mãn điều kiện cho trước 

Cách giải:
Bước 1. Tìm điều kiện của tham số để hàm số xác định.
Bước 2. Tìm các đường tiệm cận của đồ thị hàm số.
Bước 3. Giải điều kiện của bài toán để tìm tham số.
Bước 4. Kết luận

Ví dụ:

Câu 1:  Tìm tất cả các giá trị thực của tham số $m$ sao cho đồ thị của hàm số

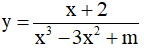
có nhiều đường tiệm cận nhất.

(Đáp án: C)

Câu 2: Số các giá trị của tham số m để đồ thị hàm số

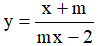
có đúng 1 tiệm cận đứng và 1 tiệm cận ngang, đồng thời hai tiệm cận này tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 18 là:

A. $0$

B. $1$

C. $2$

D. $3$
(Đáp án: C)