I. ĐỊNH NGHĨA

1) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác này gọi là đa giác nội tiếp đường tròn.

2) Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn.

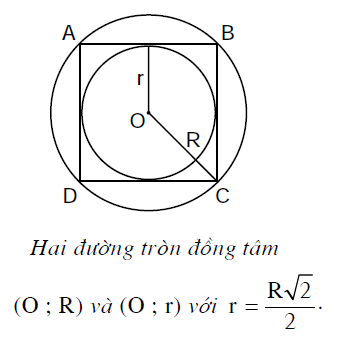
Trong hình trên ta có:

- Đường tròn $(O;R)$ là đường tròn ngoại tiếp hình vuông $ABCD$ và $ABCD$ là hình vuông nội tiếp đường tròn $(O;R).$

- Đường tròn $(O;r)$ là đường tròn nội tiếp hình vuông $ABCD$ và $ABCD$ là hình vuông ngoại tiếp đường tròn $(O;r).$

II. ĐỊNH LÍ

Bất kì đa giác đều nào cũng có một đường tròn ngoại tiếp và một đường tròn nội tiếp.

Trong đa giác đều, tâm của một đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp và được gọi là tâm của đa giác đều.