1. Định lí về hai tiếp tuyến cắt nhau

ĐỊNH LÍ

Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:

- Điểm đó cách đều hai tiếp điểm.

- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.

- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.

2. Đường tròn nội tiếp tam giác

Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.

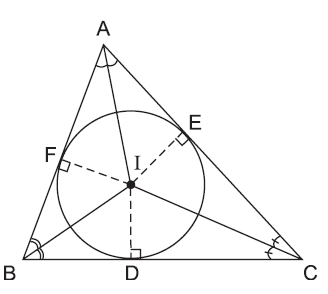
Trong hình trên, đường tròn $(I)$ nội tiếp tam giác $ABC$, tam giác $ABC$ ngoại tiếp đường tròn $(I)$.

Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác.

3. Đường tròn bàng tiếp tam giác

Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh gọi là đường tròn bàng tiếp tam giác.

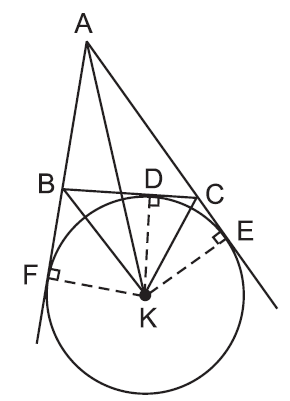
Trong hình trên, đường tròn $(K)$ bàng tiếp trong góc $A$ của tam giác $ABC$.

Tâm của đường tròn bàng tiếp tam giác trong góc $A$ là giao điểm của hai đường phân giác các góc ngoài tại $B$ và $C,$ hoặc là giao điểm của đường phân giác góc $A$ và đường phân giác góc ngoài tại $B$ (hoặc $C$).

Với một tam giác, có ba đường tròn bàng tiếp.