1. Bài toán quỹ tích “cung chứa góc”

a) Bài toán

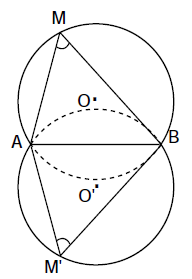
Với đoạn thẳng $AB$ và góc $α$ $({0^∘}<α<{180^∘})$ cho trước thì quỹ tích các điểm $M$ thỏa mãn $\widehat {AMB} = \alpha $ là hai cung chứa góc $α$ dựng trên đoạn $AB.$

*Chú ý :

- Hai cung chứa góc $α$ nói trên là hai cung tròn đối xứng nhau qua $AB$.

- Hai điểm $A, B$ được coi là thuộc quỹ tích.

- Quỹ tích các điểm $M$ nhìn đoạn thẳng $AB$ cho trước dưới một góc vuông là đường tròn đường kính $AB.$

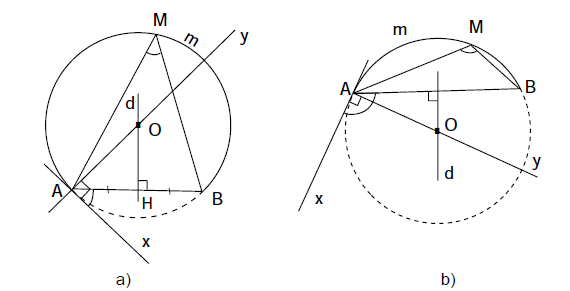
b) Cách vẽ cung chứa góc

- Vẽ đường trung trực $d$ của đoạn thẳng $AB;$

- Vẽ tia $Ax$ tạo với $AB$ một góc $α$;

- Vẽ đường thẳng $Ay$ vuông góc với $Ax$. Gọi $O$ là giao điểm của $Ay$ với $d.$

- Vẽ cung $AmB$, tâm $O$, bán kính $OA$ sao cho cung này nằm ở nửa mặt phẳng bờ $AB$ không chứa tia $Ax$. Cung $AmB$ được vẽ như trên là một cung chứa góc $α$.

2. Cách giải bài toán quỹ tích

Muốn chứng minh quỹ tích (tập hợp) các điểm $M$ thỏa mãn tính chất $T$ là một hình $H$ nào đó, ta phải chúng minh hai phần:

Phần thuận: Mọi điểm có tính chất $T$ đều thuộc hình $H$.

Phần đảo: Mọi điểm thuộc hình $H$ đều có tính chất $T$.

Kết luận: Quỹ tích (hay tập hợp) các điểm $M$ có tính chất $T$ là hình $H.$ (Thông thường với bài toán: “Tìm quỹ tích …” ta nên dự đoán hình $H$ trước khi chứng minh).