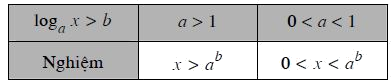1. Bất phương trình mũ

Bất phương trình mũ cơ bản có dạng:  ${a^x} > b$ (hoặc ${a^x} \ge b,{a^x} < b,{a^x} \le b$) với $a > 0,a \ne 1$.

* Xét bất phương trình dạng ${a^x} > b$.

- Nếu $b \le 0$, tập nghiệm của bất phương trình là $R$ vì ${a^x} > 0 \ge b,\forall x \in R$.

- Nếu b>0 thì bất phương trình tương đương với ${a^x} > {a^{{{\log }_a}b}}$

Với a>1, nghiệm của bất phương trình là $x > {\log _a}b$.

Với 0<a<1, nghiệm của bất phương trình là $x < {\log _a}b$.

* Vẽ đồ thị hàm số $y = {a^x}$ và đường thẳng $y = b$ trên cùng một hệ trục tọa độ.

Trong trường hợp a>1, ta nhận thấy:

- Nếu $b \le 0$, thì ${a^x} > b$ với mọi x.  

- Nếu b>0 thì ${a^x} > b$ với $x > {\log _a}b$. (Hình 10)

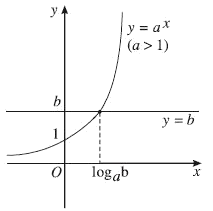
Hình 10

Trường hợp 0<a<1, ta có:

- Nếu $b \le 0$, thì ${a^x} > b$ với mọi x.  

- Nếu b>0 thì ${a^x} > b$ với $x < {\log _a}b$. (Hình 11)

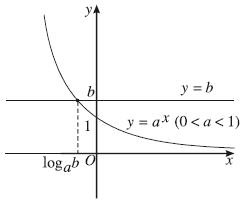
Hình 11

 * Kết luận: Tập nghiệm của bất phương trình ${a^x} > b$ được cho trong bảng sau:

2. Bất phương trình lôgarit 

Bất phương trình lôgarit cơ bản có dạng:  ${\log _a}x > b$ (hoặc ${\log _a}x \ge b,{\log _a}x \le b$) với $a > 0,a \ne 1$.

Xét bất phương trình ${\log _a}x > b$.

Trường hợp a>1, ta có ${\log _a}x > b \Leftrightarrow x > {a^b}$.

Trường hợp 0<a<1, ta có ${\log _a}x > b \Leftrightarrow x < {a^b}$.

* Vẽ đồ thị hàm số $y = {\log _a}x$ và đường thẳng $y = b$ trên cùng một hệ trục tọa độ. (Hình 12, hình 13)

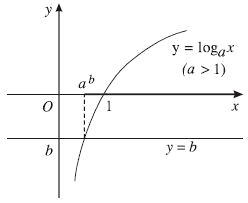
Hình 12

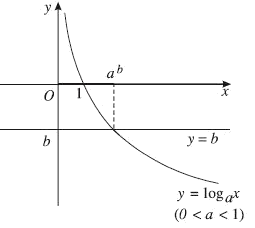
Hình 13

Quan sát đồ thị, ta thấy:

Trường hợp a>1: ${\log _a}x > b$ khi và chỉ khi $x > {a^b}$.

Trường hợp 0<a<1: ${\log _a}x > b$ khi và chỉ khi $0 < x < {a^b}$.

 * Kết luận: Nghiệm của bất phương trình ${\log _a}x > b$ được cho trong bảng sau: