I. Định nghĩa

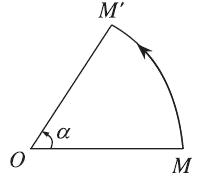
Cho điểm O và góc lượng giác $\alpha $. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM;OM’) bằng $\alpha $ được gọi là phép quay tâm O góc $\alpha $.

II. Tính chất

* Tính chất 1

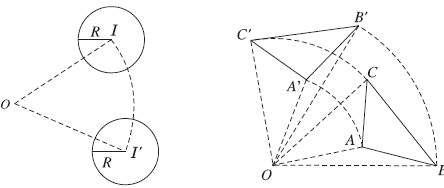
Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.

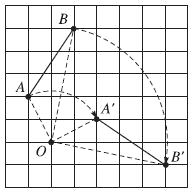
* Tính chất 2

Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

* Nhận xét

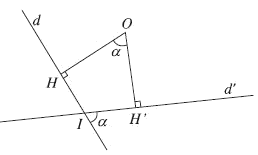
Giả sử phép quay tâm $I$ góc $\alpha $ biến đường thẳng d thành đường thẳng d’. Khi đó:

- Nếu $0 < \alpha  \le \frac{\pi }{2}$ thì góc giữa d và d’ bằng $\alpha $.

- Nếu $\frac{\pi }{2} < \alpha  < \pi $ thì góc giữa d và d’ bằng $\pi  - \alpha $.