I. Phép chiếu song song

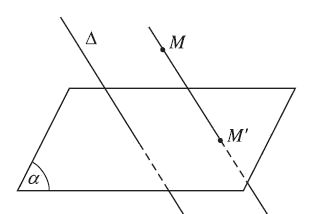
Cho mặt phẳng $\left( \alpha  \right)$ và đường thẳng $\Delta $ cắt $\left( \alpha  \right)$. Với mỗi điểm M trong không gian, đường thẳng đi qua M và song song hoặc trùng với $\Delta $ cắt $\left( \alpha  \right)$ tại điểm M’ xác định.

Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng $\left( \alpha  \right)$ theo phương $\Delta $.

Mặt phẳng $\left( \alpha  \right)$ được gọi là mặt phẳng chiếu, phương của đường thẳng $\Delta $ được gọi là phương chiếu.

Phép đặt tương ứng mỗi điểm M trong không gian với hình chiếu M’ của nó trên mặt phẳng $\left( \alpha  \right)$ được gọi là phép chiếu song song lên $\left( \alpha  \right)$ theo phương $\Delta $.

II. Tính chất của phép chiếu song song

* Định lí 1

a) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

b) Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.

* Định lí 2 (về giao tuyến của ba mặt phẳng)

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

III. Hình biểu diễn của một hình không gian trên mặt phẳng

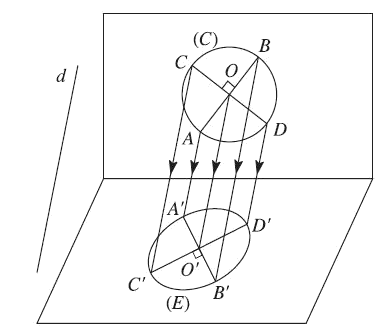
Hình biểu diễn của một hình H   trong không gian là hình chiếu song song của hình  H   trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.

* Hình biểu diễn của các hình thường gặp

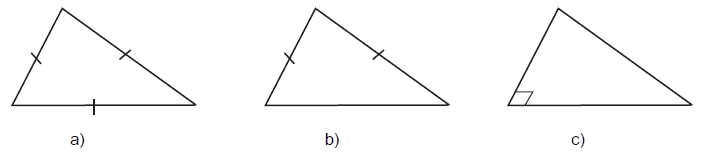
1. Một tam giác bất kì bao giờ cũng có thể coi là hình biểu diễn của một tam giác tùy ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông...).

2. Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước (có thể là hình bình hành, hình vuông, hình chữ nhật, hình thoi...)

3. Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang tùy ý cho trước, miễn là tỉ số độ dài đáy của hình biểu diễn bằng tỉ số độ dài hai đáy của hình đã cho.

4. Người ta thường dùng hình elip để biểu diễn hình tròn.