I. SƠ ĐỒ KHẢO SÁT HÀM SỐ

1. Tìm tập xác định của hàm số

2. Xét sự biến thiên của hàm số

a) Tìm giới hạn tại vô cực và giới hạn vô cực (nếu có) của hàm số.

Tìm các đường tiệm cận của đồ thị (nếu có).

b) Lập bảng biến thiên của hàm số, bao gồm:

Tìm đạo hàm của hàm số, xét dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng.

3. Vẽ đồ thị của hàm số

* Vẽ các đường tiệm cận của đồ thị (nếu có).

* Xác định một số điểm đặc biệt của đồ thị, chẳng hạn tìm giao điểm của đồ thị với các trục toạ độ. (Trong trường hợp đồ thị không cắt các trục tọa độ hoặc việc tìm tọa độ giao điểm phức tạp thì bỏ qua phần này).

* Nhận xét về đồ thị : Chỉ ra trục và tâm đối xứng của đồ thị (nếu có, không yêu cầu chứng minh).

II. KHẢO SÁT MỘT SỐ HÀM ĐA THỨC VÀ HÀM PHÂN THỨC

1. Dạng của đồ thị hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$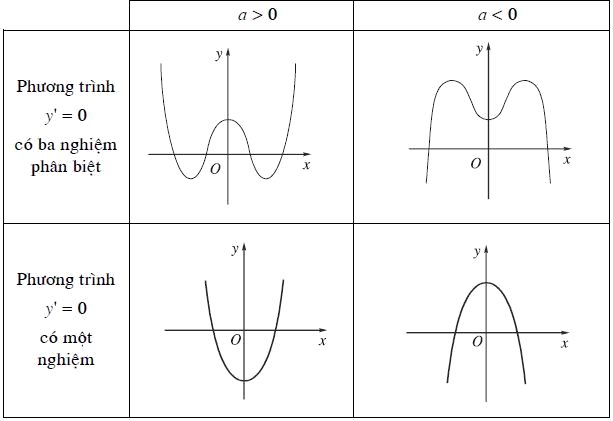


























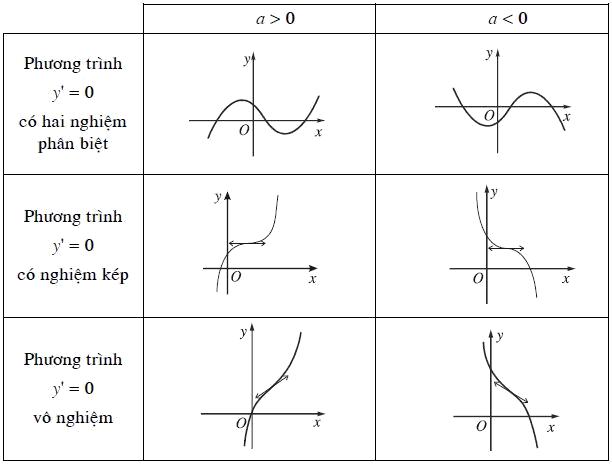
2. Dạng của đồ thị hàm số $y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)$

3. Dạng của đồ thị hàm số $y = \frac{{ax + b}}{{cx + d}}\left( {a,c \ne 0} \right)$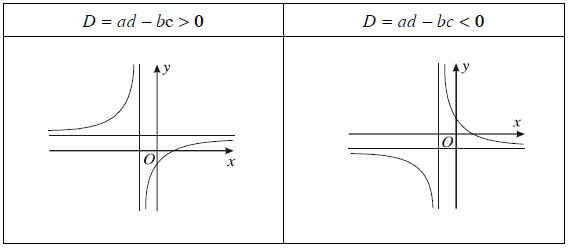














III. SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ

* Ví dụ: Tìm tọa độ giao điểm của đồ thị hai hàm số
$\begin{array}{l}y = {x^2} + 2x - 3\\y =  - {x^2} - x + 2\end{array}$

Giải

Giả sử hàm số $y = f\left( x \right)$ có đồ thị là $\left( {{C_1}} \right)$ và hàm số $y = g\left( x \right)$ có đồ thị là  $\left( {{C_2}} \right)$. Để tìm hoành độ giao điểm của $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$, ta phải giải phương trình $f\left( x \right) = g\left( x \right)$. Giả sử phương trình trên có các nghiệm là ${x_0},{x_1},...$ Khi đó, các giao điểm của $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ lần lượt là ${M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right),{M_1}\left( {{x_1};f\left( {{x_1}} \right)} \right),...$