Khái niệm hệ số góc của đường thẳng $y = ax + b (a \ne 0)$

1. Góc tạo bởi đường thẳng $y=ax+b$ và trục $Ox$

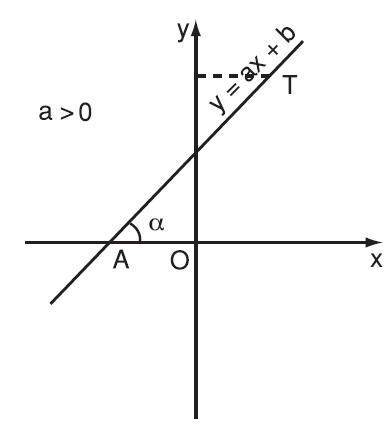
Trong mặt phẳng tọa độ $Oxy$, khi nói góc $\alpha $ tạo bởi đường thẳng $y=ax+b$ và trục $Ox$ (hoặc nói đường thẳng $y=ax+b$ tạo với trục $Ox$ một góc $\alpha $), ta hiểu đó là góc tạo bởi tia $Ax$ và tia $AT$, trong đó $A$ là giao điểm của đường thẳng $y=ax+b$ với trục $Ox,T$ là điểm thuộc đường thẳng $y=ax+b$ và có tung độ dương.

Hình biểu diễn đồ thị của hàm số $y=ax+b$ với hệ số $a>0$

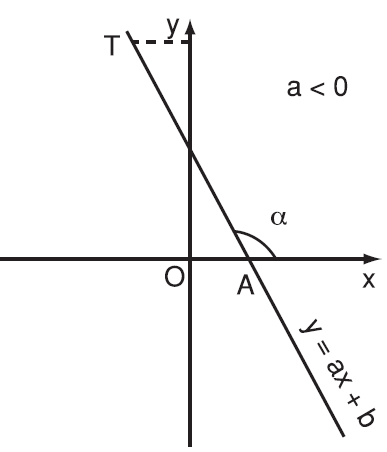
Hình biểu diễn đồ thị của hàm số $y=ax+b$ với hệ số $a<0$

2. Hệ số góc

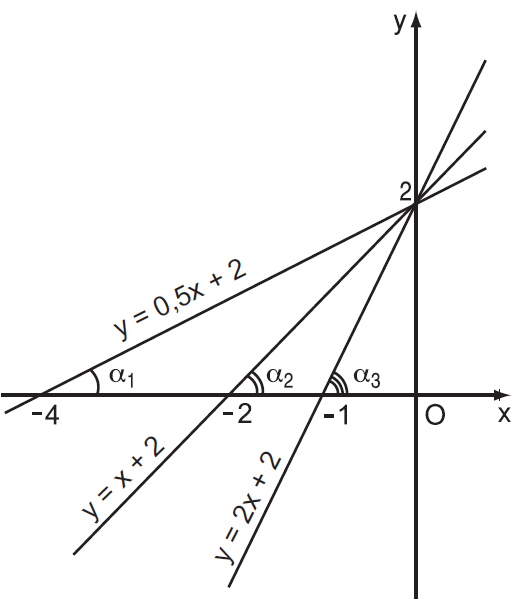
Các đường thẳng có cùng hệ số $a$ ($a$ là hệ số của $x$) thì tạo với trục $Ox$ các góc bằng nhau.

Hình biểu diễn đồ thị của các hàm số với hệ số $a>0$

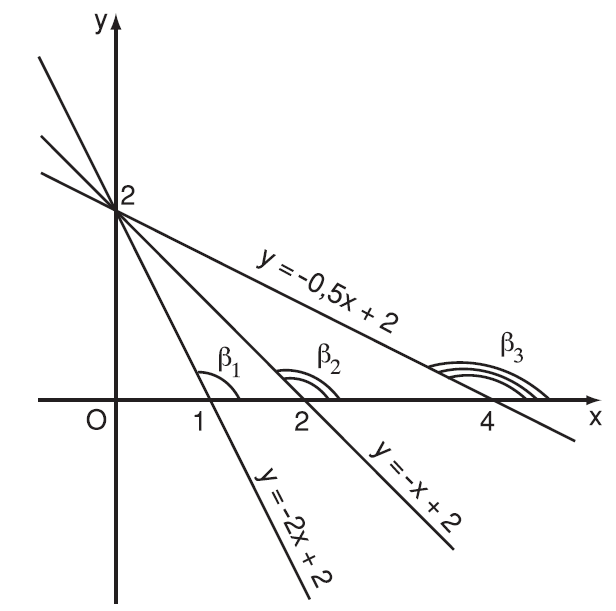
Hình biểu diễn đồ thị của các hàm số với hệ số $a<0$

* Chú ý: Khi $b=0$, ta có hàm số $y=ax$. Trong trường hợp này, ta cũng nói rằng $a$ là hệ số góc của đường thẳng $y=ax$.