1. Góc có đỉnh bên trong đường tròn

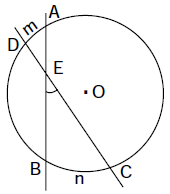
Góc $BEC$ có đỉnh $E$ nằm bên trong đường tròn $(O)$ được gọi là góc có đỉnh ở bên trong đường tròn.

ĐỊNH LÝ

Số đo của góc đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

2. Góc có đỉnh bên ngoài đường tròn

Góc có đỉnh nằm bên ngoài đường tròn và các cạnh đều có điểm chung với đường tròn. Mỗi góc đó được gọi là góc có đỉnh ở bên ngoài đường tròn. Mỗi góc có đỉnh ở bên ngoài đường tròn có hai cung bị chắn, đó là hai cung nằm bên trong góc.  

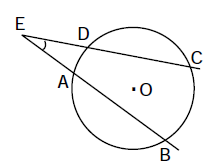
Góc $BEC$ có hai cạnh cắt đường tròn, hai cung bị chắn là hai cung nhỏ $AD$ và $BC.$

Góc $BEC$ có một cạnh là tiếp tuyến tại $C$ và cạnh kia là cát tuyến, hai cung bị chắn là hai cung nhỏ $AC$ và $CB.$

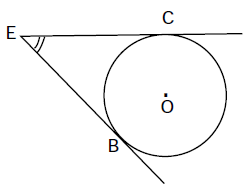
Góc $BEC$ có hai cạnh là hai tiếp tuyến tại $B$ và $C,$ hai cung bị chắn là hai cung nhỏ $BC$ và $BC.$

ĐỊNH LÝ

Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.