1. Ba vị trí tương đối của đường thẳng và đường tròn

            a)  Đường thẳng và đường tròn cắt nhau

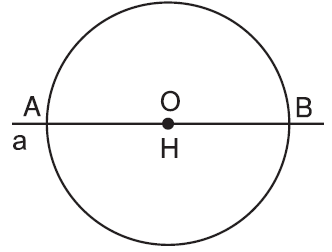
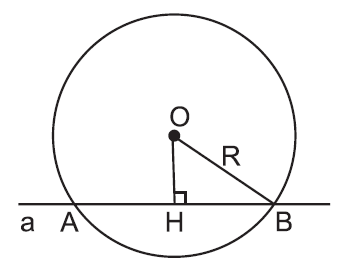
- Khi đường thẳng $a$ và đường tròng $(O)$ có hai điểm chung $A$ và $B$, ta nói đường thẳng $a$ và đường tròn $(O)$ cắt nhau. (Đường thẳng $a$ còn gọi là cát tuyến của đường tròn $(O)$).

- Khi $OH<R$ và $HA = HB = \sqrt {{R^2} - O{H^2}} .$

             b) Đường thẳng và đường tròn tiếp xúc nhau

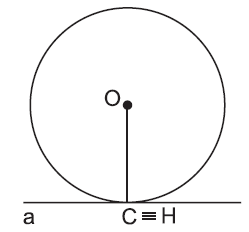
- Khi đường thẳng $a$ và đường tròng $(O)$ chỉ có một điểm chung $C,$ ta nói đường thẳng $a$ và đường tròn $(O)$ tiếp xúc nhau. (Đường thẳng $a$ còn gọi là tiếp tuyến của đường tròn $(O)$ và $C$ gọi là tiếp điểm).

- Khi $H$ trùng với $C$, $OC \bot a$ và $OH=R.$

ĐỊNH LÍ

Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

             c) Đường thẳng và đường tròn không giao nhau

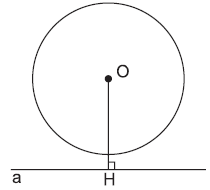
- Khi đường thẳng $a$ và đường tròng $(O)$ không có điểm chung, ta nói đường thẳng $a$ và đường tròn $(O)$ không giao nhau.

- Khi đó $OH>R.$

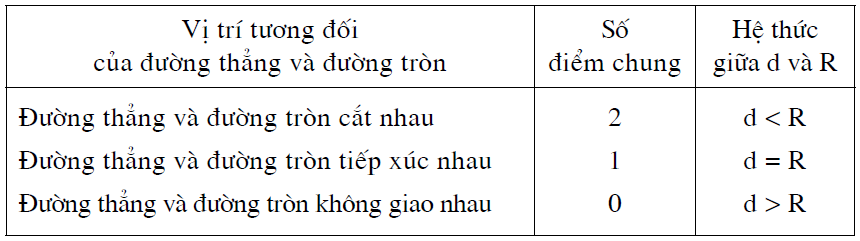
2. Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn