I. Lũy thừa

Lũy thừa với số mũ tự nhiên

Lũy thừa bậc $n$ của $a$ là tích của $n$ thừa số bằng nhau, mỗi thừa số bằng $a$:

$a^n=a.a…..a$ ($n$ thừa số $a$) ($n$ ∉ $N^∗$ )

$a^n$ đọc là “$a$ mũ $n$” hoặc “$a$ lũy thừa $n$”.

$a$  được gọi là cơ số.

$n$ được gọi là số mũ.

Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.

$a^1=a$

$a^2=a.a$  gọi là “$a$ bình phương”  (hay bình phương của $a$).

$a^3=a.a.a$  gọi là “$a$ lập phương” (hay lập phương của $a$).

Với $n$ là số tự nhiên khác $0$ (thuộc $N^∗$), ta có: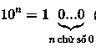 
  (số mũ là $n$ thì có $n$ chữ số $0$ đằng sau chữ số $1$)

Quy ước: $a^1=a$; $a^o=1$ (a≠0).

II. Nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

$a^m.a^n=a^{m+n}$

III. Chia hai lũy thừa cùng cơ số

Khi chia hai lũy thừa cùng cơ số (khác $0$), ta giữ nguyên cơ số và trừ các số mũ cho nhau.

$a^m:a^n=a^{m−n}$ (a≠0;m≥n≥0)

Lưu ý:

Phép chia hai lũy thừa cùng cơ số không thể lấy hai số mũ chia cho nhau mà phải lấy hai số mũ trừ cho nhau.