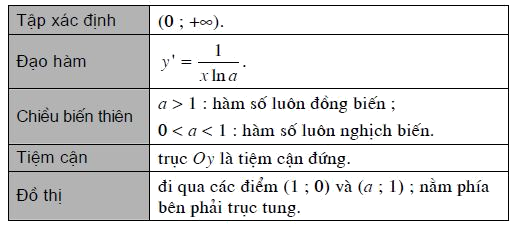I. Hàm số mũ

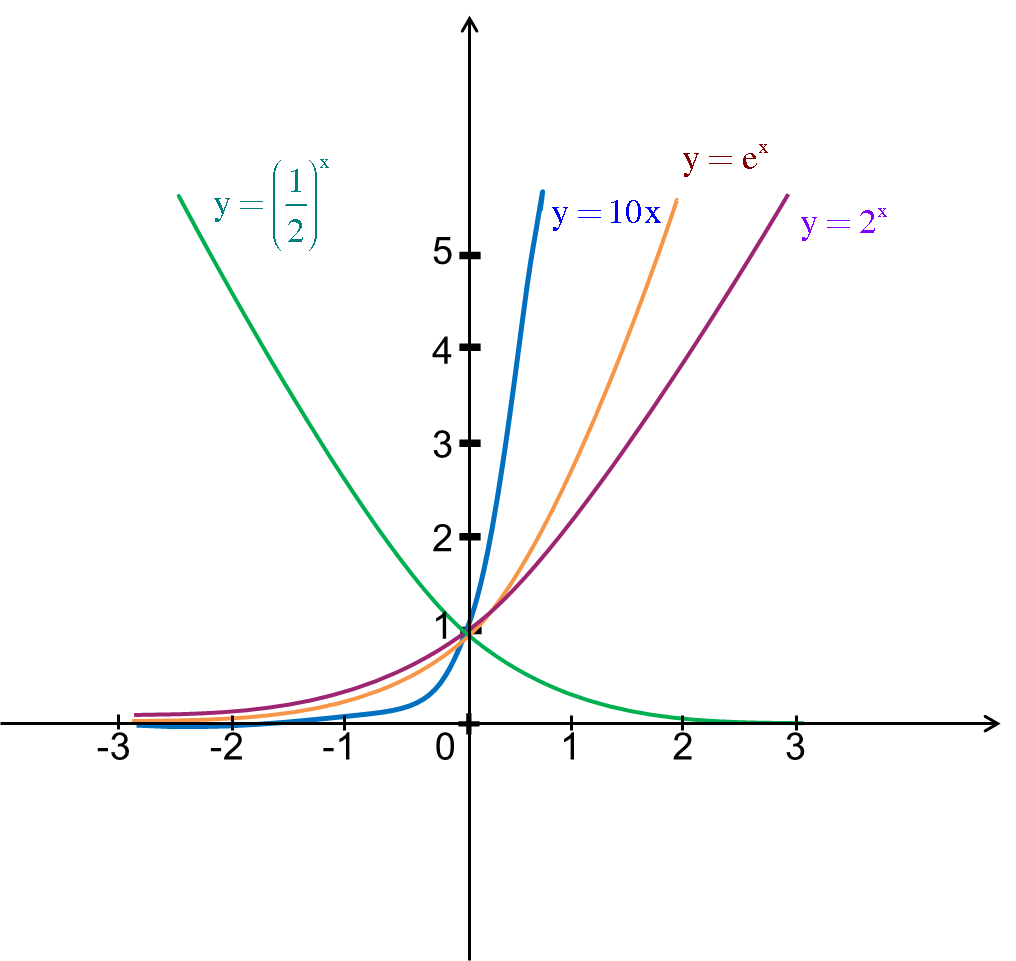
Cho số thực dương a khác 1. Hàm số $y = {a^x}$ được gọi là hàm số mũ cơ số a.

* Đạo hàm của hàm số mũ

Định lí 1:

Hàm số $y = {e^x}$ có đạo hàm tại mọi x và $\left( {{e^x}} \right)' = {e^x}$.

Định lí 2:

Hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$ có đạo hàm tại mọi x và $\left( {{a^x}} \right)' = {a^x}\ln a$.

* Khảo sát hàm số mũ $y = {a^x}\left( {a > 0,a \ne 1} \right)$

1. $y = {a^x},a > 1$

- Tập xác định:  $R$

- Sự biến thiên:
 $y = {a^x}\ln a > 0,\forall x$

Giới hạn đặc biệt:
 $\mathop {\lim }\limits_{x \to  - \infty } {a^x} = 0,\mathop {\lim }\limits_{x \to  + \infty } {a^x} =  + \infty $

Tiệm cận:

Trục Ox là tiệm cận ngang.

- Bảng biến thiên: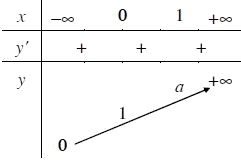

- Đồ thị (Hình 06)

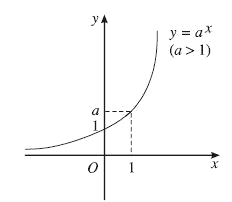
Hình 06

2. $y = {a^x},0 < a < 1$

- Tập xác định: $R$

- Sự biến thiên:
 $y = {a^x}\ln a < 0,\forall x$

Giới hạn đặc biệt:

  $\mathop {\lim }\limits_{x \to  - \infty } {a^x} =  + \infty ,\mathop {\lim }\limits_{x \to  + \infty } {a^x} = 0$

Tiệm cận:

Trục Ox là tiệm cận ngang.

- Bảng biến thiên:

- Đồ thị (Hình 07)

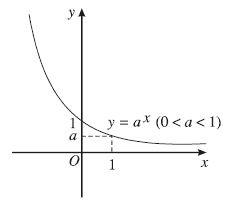
Hình 07

Bảng tóm tắt các tính chất của hàm số mũ $y = {a^x}\left( {a > 0,a \ne 1} \right)$

II. Hàm số lôgarit

Cho số thực dương a khác 1. Hàm số $y = {\log _a}x$ được gọi là hàm số lôgarit cơ số a.

* Đạo hàm của hàm số mũ

Định lí 3:

Hàm số $y = {\log _a}x\left( {a > 0,a \ne 1} \right)$ có đạo hàm tại mọi x>0 và $\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}}$.

Đặc biệt:
 $\left( {\ln x} \right)' = \frac{1}{x}$

* Khảo sát hàm số mũ $y = {\log _a}x\left( {a > 0,a \ne 1} \right)$

1. $y = {\log _a}x,a > 1$

- Tập xác định: $\left( {0; + \infty } \right)$

- Sự biến thiên:
 $y' = \frac{1}{{x\ln a}} > 0,\forall x > 0$

Giới hạn đặc biệt:
 $\mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x =  - \infty ,\mathop {\lim }\limits_{x \to  + \infty } {\log _a}x =  + \infty $

Tiệm cận:

Trục Oy là tiệm cận đứng.

- Bảng biến thiên:

- Đồ thị (Hình 08)

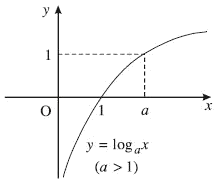
Hình 08

2. $y = {\log _a}x,0 < a < 1$

- Tập xác định: $\left( {0; + \infty } \right)$

- Sự biến thiên:
 $y' = \frac{1}{{x\ln a}} < 0,\forall x > 0$

Giới hạn đặc biệt:
 $\mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x =  + \infty ,\mathop {\lim }\limits_{x \to  + \infty } {\log _a}x =  - \infty $

Tiệm cận:

Trục Oy là tiệm cận đứng.

- Bảng biến thiên:

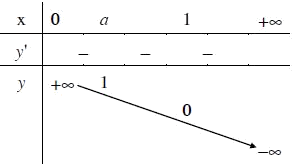
- Đồ thị (Hình 09)

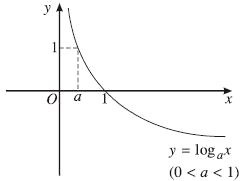
Hình 09

Bảng tóm tắt các tính chất của hàm số $y = {\log _a}x\left( {a > 0,a \ne 1} \right)$