I. Góc giữa hai mặt phẳng

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

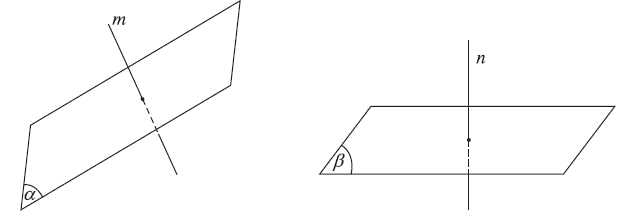
* Cách xác định góc giữa hai mặt phẳng cắt nhau  

Cho hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$ cắt nhau theo giao tuyến c. Từ một điểm $I$ bất kì trên c ta dựng đường thẳng a trong $\left( \alpha  \right)$ vuông góc với c và dựng đường thẳng b trong $\left( \beta  \right)$ vuông góc với c. Khi đó góc giữa $\left( \alpha  \right)$ và $\left( \beta  \right)$ là góc giửa hai đường thẳng a và b.

* Diện tích hình chiếu của đa giác:

$S' = S\cos \varphi $

Với S là diện tích đa giác nằm trong $\left( \alpha  \right)$, S’ là diện tích hình chiếu vuông góc của đa giác đó trên $\left( \beta  \right)$, $\varphi $ là góc giữa $\left( \alpha  \right)$ và $\left( \beta  \right)$.

II. Hai mặt phẳng vuông góc

1. Định nghĩa

Hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$ được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là một góc vuông.

Khi đó ta kí hiệu $\left( \alpha  \right) \bot \left( \beta  \right)$ hoặc $\left( \beta  \right) \bot \left( \alpha  \right)$.

2. Các định lí  

* Định lí 1

Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

* Hệ quả 1

Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.

* Hệ quả 2

Cho hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$ vuông góc nhau. Nếu từ một điểm thuộc mặt phẳng $\left( \alpha  \right)$ ta dựng một đường thẳng vuông góc với mặt phẳng $\left( \beta  \right)$ thì đường thẳng này nằm trong mặt phẳng $\left( \alpha  \right)$.

* Định lí 2

Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.  

III. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương

Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với các mặt đáy.

Hình hộp chữ nhật là hình trụ đứng có đáy là hình chữ nhật.

Hình lập phương là hình trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông.

IV. Hình chóp đều và hình chóp cụt đều

Hình chóp đều là hình chóp có đáy là một đa giác đều và có chân đường cao trùng với tâm của đa giác đáy.

Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với đáy cắt tất cả các cạnh bên của hình chóp đều được gọi là hình chóp cụt đều.