1. Định nghĩa

Cho hai điểm cố định ${F_1},{F_2}$ và một độ dài không đổi 2a lớn hơn ${F_1}{F_2}$. Elip là tập hợp các điểm M trong mặt phẳng sao cho

${F_1}M + {F_2}M = 2a$

Các điểm ${F_1}$ và ${F_2}$ gọi là các tiêu điểm của elip. Độ dài ${F_1}{F_2} = 2c$ gọi là tiêu cự của elip.

2. Phương trình chính tắc của elip

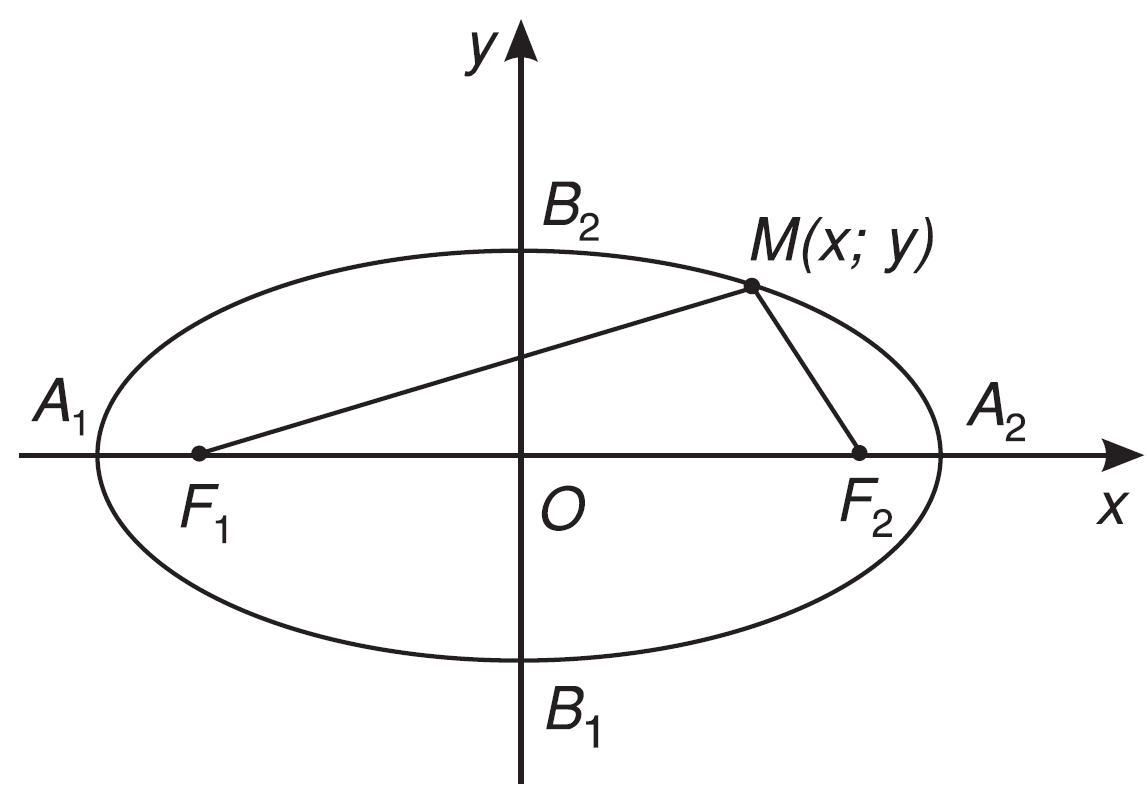
Cho elip (E) có các tiêu điểm ${F_1}$ và ${F_2}$. Điểm M thuộc elip khi và chỉ khi ${F_1}M + {F_2}M = 2a$. Chọn hệ trục toạ độ Oxy sao cho ${F_1} = \left( { - c;0} \right)$ và ${F_2} = \left( {c;0} \right)$. Khi đó người ta chứng minh được:

$M\left( {x;y} \right) \in E \Leftrightarrow \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$

trong đó ${b^2} = {a^2} - {c^2}$.

Phương trình (1) gọi là phương trình chính tắc của elip.

3. Hình dạng của elip

Xét elip (E) có phương trình (1) :

* Nếu điểm M(x ; y) thuộc (E) thì các điểm ${M_1} = \left( { - x;y} \right),{M_2} = \left( {x; - y} \right)$ cũng thuộc (E).

Vậy (E) có các trục đối xứng là Ox, Oy và có tâm đối xứng là gốc O.

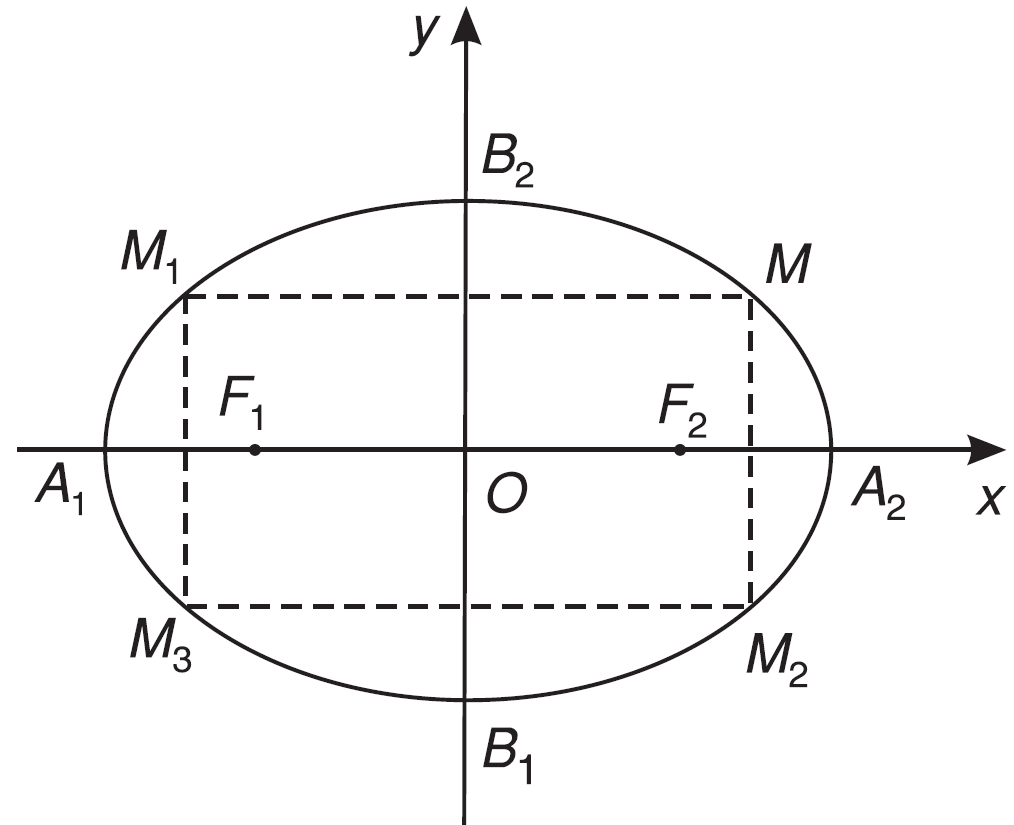
* Thay y = 0 vào (1) ta có x = ±a, suy ra (E) cắt Ox tại hai điểm ${A_1} = \left( { - a;0} \right)$ và ${A_2} = \left( {a;0} \right)$.

Tương tự thay x = 0 vào (1) ta được y = ±b, vậy (E) cắt Oy tại hai điểm ${B_1} = \left( {0; - a} \right),{B_2} = \left( {0;b} \right)$.

Các điểm ${A_1},{A_2},{B_1},{B_2}$ gọi là các đỉnh của elip.

Đoạn thẳng ${A_1}{A_2}$ gọi là trục lớn, đoạn thẳng ${B_1}{B_2}$ gọi là trục nhỏ của elip.

4. Liên hệ giữa đường tròn và đường elip

* Từ hệ thức ${b^2} = {a^2} - {c^2}$ ta thấy nếu tiêu cự của elip càng nhỏ thì b càng gần bằng a, tức là trục nhỏ của elip càng gần bằng trục lớn. Lúc đó elip có dạng gần như đường tròn.

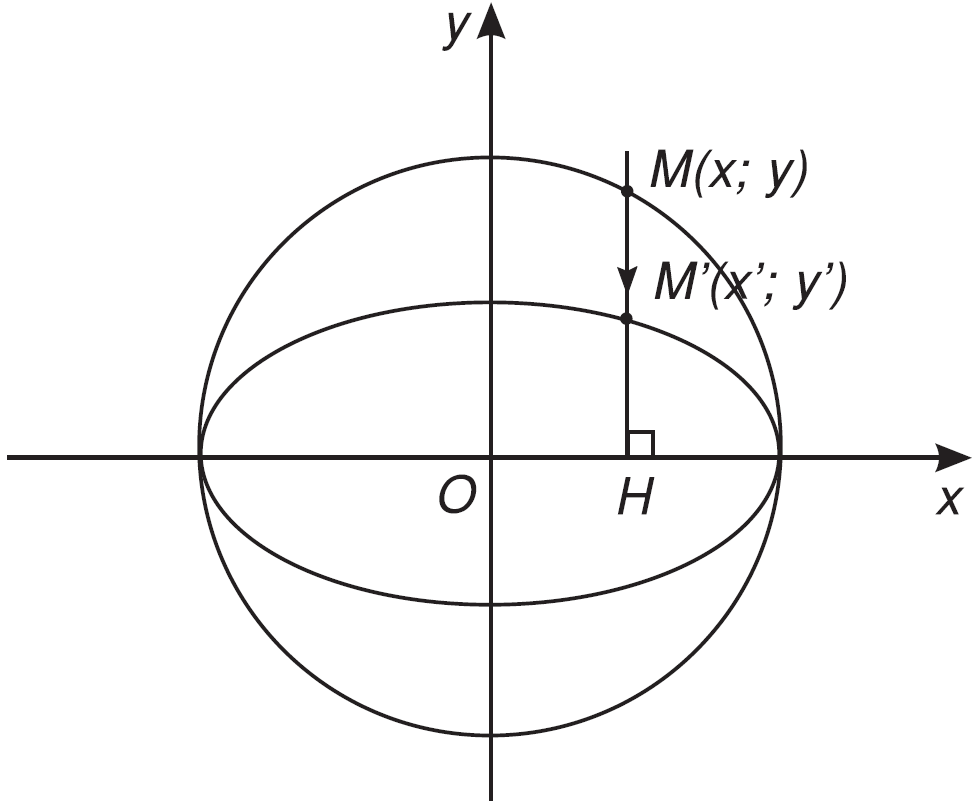
* Trong mặt phẳng Oxy cho đường tròn (C ) có phương trình

${x^2} + {y^2} = {a^2}$

Với mỗi điểm M(x ; y) thuộc đường tròn ta xét điểm M’(x’ ; y’) sao cho

$\left\{ \begin{gathered}   x' = x \hfill \\   y' = \frac{b}{a}y \hfill \\ \end{gathered}  \right.\left( {0 < b < a} \right)$

thì tập hợp các điểm M' có toạ độ thoả mãn phương trình $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ là một elip (E).

Khi đó ta nói đường tròn (C) được co thành elip (E).