1. Định nghĩa

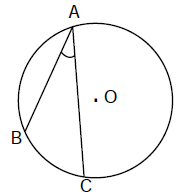
- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

- Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn.

Ví dụ:

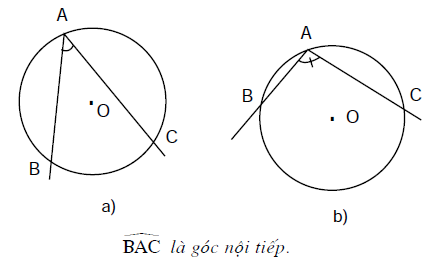
Trong hình trên:

a) Cung bị chắn là cung nhỏ $BC$;

b) Cung bị chắn là cung lớn $BC.$

2. Định lý

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Cần phân biệt 3 trường hợp:

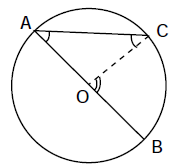
- Tâm đường tròn nằm trên một cạnh của góc.

- Tâm đường tròn nằm bên trong góc.

- Tâm đường tròn nằm bên ngoài góc.

3. Hệ quả

Trong một đường tròn:

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

c) Góc nội tiếp (nhỏ hơn hoặc bằng $90^∘$) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.

d) Góc nội tiếp chắn nửa đường tròn là góc vuông.