1. Đồ thị của hàm số y = ax + b (a \ne 0)$

Đồ thị của hàm số $y=ax+b (a \ne 0)$ là một đường thẳng:

- Cắt trục tung tại điểm có tung độ bằng $b$;

- Song song với một đường thẳng $y=ax$, nếu $b \ne 0;$ trùng với đường thẳng $y=ax$, nếu $b=0.$

2. Cách vẽ đồ thị của hàm số $y = ax + b (a \ne 0)$

- Khi $b=0$ thì $y=ax$. Đồ thị của hàm số $y=ax$ là đường thẳng đi qua gốc tọa độ $O(0;0)$ và điểm $A(1;a).$

- Xét trường hợp $y=ax+b$ với $a \ne 0$ và $b \ne 0.$

Đồ thị của hàm số $y=ax+b$ là một đường thẳng. Do đó, để vẽ đồ thị hàm số $y=ax+b$ ta chỉ cần xác định được hai điểm phân biệt nào đó thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó (Ta thường xác định hai điểm đặc biệt là giao điểm của đồ thị với hai trục tọa độ).

+Bước 1:

Cho $x=0$ thì $y=b,$ ta được điểm $P(0;b)$ thuộc trục tung $Oy.$

Cho $y=0$ thì $x= - \frac{b}{a}$, ta được điểm $Q\left( { - \frac{b}{a};0} \right)$ thuộc trục hoành $Ox.$

+Bước 2:

Vẽ đường thẳng đi qua hai điểm $P$ và $Q$ ta được đồ thị của hàm số $y=ax+b.$

Vì dụ:

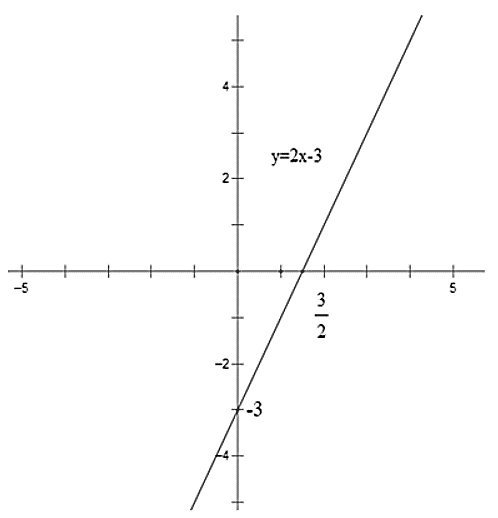
Vẽ đồ thị của hàm số $y=2x-3$

- Cho $x = 0 \Rightarrow y = 2.0 - 3 =  - 3 \Rightarrow A\left( {0; - 3} \right)$

- Cho $y = 0 \Rightarrow 0 = 2x - 3 \Rightarrow x = \frac{3}{2} \Rightarrow B\left( {\frac{3}{2};0} \right)$

Do đó đồ thị hàm số là đường thẳng đi qua hai điểm $A\left( {0; - 3} \right)$ và $B\left( {\frac{3}{2};0} \right)$