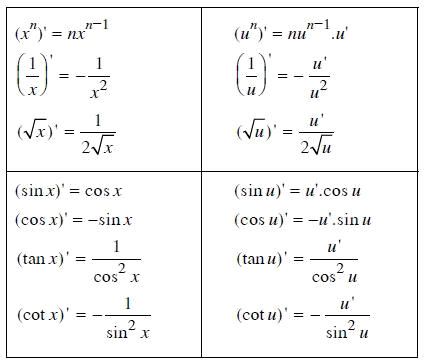1. Giới hạn của $\frac{{\sin x}}{x}$

* Định lí 1

$\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1$

2. Đạo hàm của hàm số $y = \sin x$

* Định lí 2

Hàm số $y = \sin x$ có đạo hàm tại mọi ${x \in R}$ và $\left( {\sin x} \right)' =  - \cos x$.

3. Đạo hàm của hàm số $y = \cos x$

* Định lí 3

Hàm số $y = \cos x$ có đạo hàm tại mọi ${x \in R}$ và $\left( {\cos x} \right)' =  - \sin x$.

4. Đạo hàm của hàm số $y = \tan x$

* Định lí 4

Hàm số $y = \tan x$ có đạo hàm tại mọi $x \ne \frac{\pi }{2} + k\pi ,k \in Z$  và

$\left( {tanx} \right)' =  - \frac{1}{{{{\cos }^2}x}}$.

5. Đạo hàm của hàm số $y = \cot x$

* Định lí 5

Hàm số $y = \cot x$ có đạo hàm tại mọi $x \ne k\pi ,k \in Z$  và

$\left( {\cot x} \right)' =  - \frac{1}{{{{\sin }^2}x}}$.

Bảng đạo hàm