1. Định lí côsin

a) Định lí

Trong tam giác ABC bất kì với BC = a, CA = b; AB = c ta có:

$\begin{gathered}   {a^2} = {b^2} + {c^2} - 2bc\cos A; \hfill \\   {b^2} = {a^2} + {c^2} - 2ac\cos B; \hfill \\   {c^2} = {a^2} + {b^2} - 2ab\cos C. \hfill \\ \end{gathered} $

b) Hệ quả

$\begin{gathered}   \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}; \hfill \\   cosB = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}; \hfill \\   \cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}. \hfill \\ \end{gathered} $.

c) Áp dụng

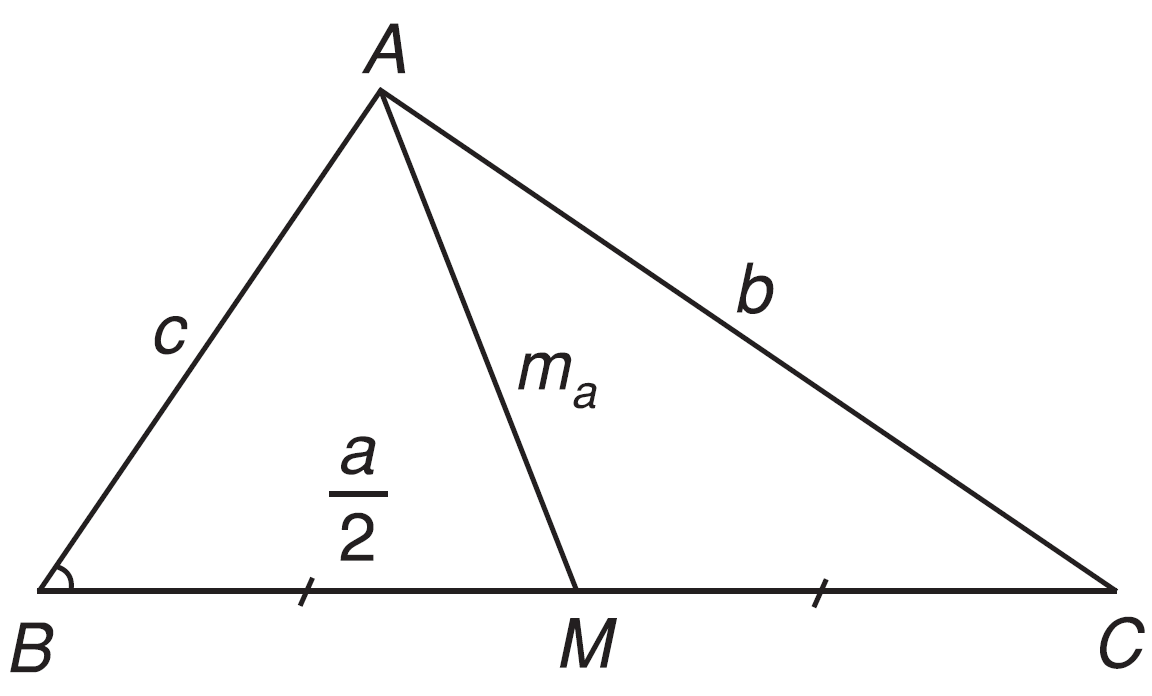
$\begin{gathered}   m_a^2 = \frac{{2\left( {{b^2} + {c^2}} \right) - {a^2}}}{4}; \hfill \\   m_b^2 = \frac{{2\left( {{a^2} + {c^2}} \right) - {b^2}}}{4}; \hfill \\   m_c^2 = \frac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4}. \hfill \\ \end{gathered} $.

2. Định lí sin

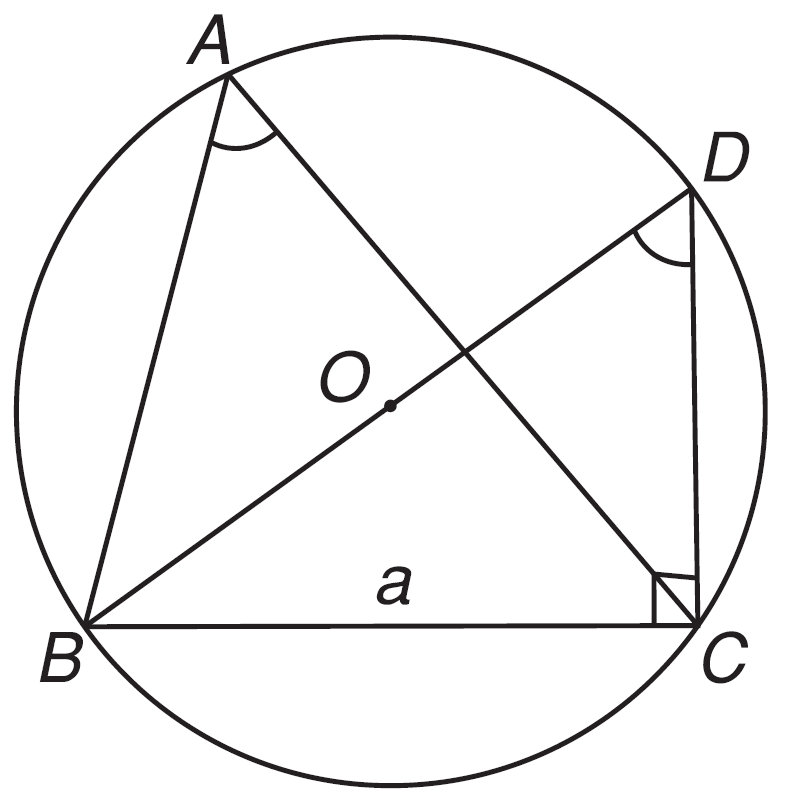
Trong tam giác ABC bất kì với BC = a, CA = b; AB = c và R là bán kính đường tròn ngoại tiếp, ta có:

$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$.

3. Công thức tính diện tích tam giác

Diện tích S của tam giác ABC được tính theo một trong các công thức sau:

$S = \frac{1}{2}ab\sin C = \frac{1}{2}bc\operatorname{sinA}  = \frac{1}{2}ca\sin B(1);$

$S = \frac{{abc}}{{4R}}(2);$

$S = pr(3);$

$S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} (4)$ (công thức Hê - rông).

4. Giải tam giác và ứng dụng vào việc đo đạc

Giải tam giác là tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.

Muốn giải tam giác ta thường sử dụng các hệ thức đã được nêu lên trong định lí côsin, định lí sin và các công thức tính diện tích tam giác.