Trong bài học này chúng ta sẽ làm quen với khái niệm tích phân. Đây là khái niệm cơ bản, quan trọng của giải tích, có liên hệ mật thiết với khái niệm đạo hàm. Phép tính tích phân cho chúng ta một phương pháp tổng quát để tích diện tích của những hình phẳng và thể tích của những vật thể có hình dạng phức tạp. Phép tính tích phân được xem là một trong những thành tựu quan trọng nhất của toán học.

I. Khái niệm tích phân

1. Diện tích hình thang cong

Khái niệm tích phân được bắt nguồn từ những bài toán thực tế. Chẳng hạn, bài toán tính diện tích hình thang cong.

Cho hàm số $y = f\left( x \right)$ liên tục, không đổi trên đoạn $\left[ {a;b} \right]$. Hình phẳng giới hạn bởi đồ thị của hàm số $y = f\left( x \right)$, trục hoành và hai đường thẳng $x = a,x = b$ được gọi là hình thang cong.

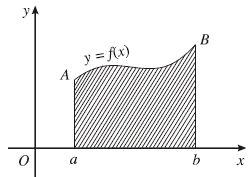
Khái niệm hình thang cong giúp ta giải bài toán tìm diện tích một hình phẳng được giới hạn bởi một đường cong khép kín (vì nó bằng tổng diện tích của một số hình thang cong dạng này hay dạng khác), bằng cách chuyển từ một bài toán phức tạp về bài toán đơn giản.

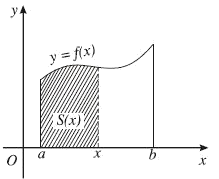
2. Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn $\left[ {a;b} \right]$. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn $\left[ {a;b} \right]$.

Hiệu số F(b) - F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn $\left[ {a;b} \right]$) của hàm số f(x) kí hiệu là:

$\int\limits_a^b {f\left( x \right)dx} $

II. Tính chất của tích phân

* Tính chất 1

$\int\limits_a^b {kf\left( x \right)dx}  = k\int\limits_a^b {f\left( x \right)dx} $

(k là hằng số)

* Tính chất 2

$\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx}  = \int\limits_a^b {f\left( x \right)dx}  \pm \int\limits_a^b {g\left( x \right)dx} $

* Tính chất 3

$\int\limits_a^b {f\left( x \right)dx}  = \int\limits_a^c {f\left( x \right)dx}  + \int\limits_c^b {f\left( x \right)dx} $

(a < c < b).

Ví dụ: Tính tích phân $I = \int\limits_0^2 {\left| {x - 1} \right|dx.} $

Phân tích: Ta có bảng xét dấu của $x-1$ trên đoạn $\left[ {0;2} \right].$


Trên đoạn $\left[ {0;1} \right]$ thì $x - 1 \leqslant 0$ nên $\left| {x - 1} \right| = 1 - x.$

Trên đoạn $\left[ {1;2} \right]$ thì $x - 1 \geqslant 0$ nên $\left| {x - 1} \right| = x - 1.$

Giải

$\begin{array}{l}
I = \int\limits_0^2 {\left| {x - 1} \right|} dx = \int\limits_0^1 {\left| {x - 1} \right|} dx + \int\limits_1^2 {\left| {x - 1} \right|} dx\\
 = \int\limits_0^1 {\left( {x - 1} \right)} dx + \int\limits_1^2 {\left( {x - 1} \right)} dx\\
 = \left( {x - \frac{{{x^2}}}{2}} \right)\left| {_0^1} \right. + \left( {\frac{{{x^2}}}{2} - x} \right)\left| {_1^2} \right. = 1.
\end{array}$


Lưu ý: Trong ví dụ này ta có thể không cần quan tâm đến dấu của $x-1$ mà chỉ cần đưa dấu trị tuyệt đối ra ngoài tích phân và giải như sau:

$\begin{array}{l}
I = \int\limits_0^2 {\left| {x - 1} \right|} dx = \int\limits_0^1 {\left| {x - 1} \right|} dx + \int\limits_1^2 {\left| {x - 1} \right|} dx\\
 = \left| {\int\limits_0^1 {\left( {x - 1} \right)} dx} \right| + \left| {\int\limits_1^2 {\left( {x - 1} \right)} dx} \right|\\
 = \left| {\left( {x - \frac{{{x^2}}}{2}} \right)\left| {_0^1} \right.} \right| + \left| {\left( {\frac{{{x^2}}}{2} - x} \right)\left| {_1^2} \right.} \right|\\
 = \left| {\frac{1}{2}} \right| + \left| { - \frac{1}{2}} \right| = 1.
\end{array}$

III. Phương pháp tính tích phân

1. Phương pháp đổi biến số:

Định lí

Cho f(x) là hàm số liên tục trên đoạn $\left[ {a;b} \right]$. Giả sử hàm số $x = \varphi \left( t \right)$ có đạo hàm liên tục trên đoạn $\left[ {\alpha ;\beta } \right]$ sao cho $\varphi \left( \alpha  \right) = a,\varphi \left( \beta  \right) = b$ và $a \le \varphi \left( t \right) \le b$ với mọi $t \in \left[ {\alpha ;\beta } \right]$.

Khi đó:

$\int\limits_a^b {f\left( x \right)dx}  = \int\limits_\alpha ^\beta  {f\left( {\varphi \left( x \right)} \right)\varphi '\left( t \right)dt} $

2. Phương pháp tính tích phân từng phần:

Định lí

Nếu $u = u\left( x \right)$ và $v = v\left( x \right)$ là hai hàm số có đạo hàm liên tục trên đoạn $\left[ {a;b} \right]$ thì:

$\int\limits_a^b {u\left( x \right)v'\left( x \right)dx}  = \left. {\left( {u\left( x \right)v\left( x \right)} \right)} \right|_a^b - \int\limits_a^b {u'\left( x \right)v\left( x \right)dx} $

Hay:

$\int\limits_a^b {udv}  = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} $