I. Ôn tập về phương trình bậc nhất, bậc hai

1. Phương trình bậc nhất

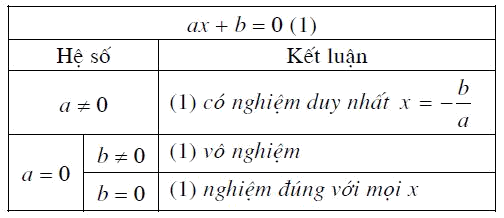
2. Phương trình bậc hai

3. Định lí Viet

Nếu phương trình bậc hai $y = a{x^2} + bx + c\left( {a \ne 0} \right)$ có hai nghiệm ${x_1},{x_2}$ thì:

${x_1} + {x_2} =  - \frac{b}{a};{x_1}{x_2} = \frac{c}{a}$

Ngược lại, nếu hai số u và v có tổng u + v = S và tích uv = P thì u và v là các nghiệm của phương trình

${x^2} - Sx + P = 0$

II. Phương trình quy về phương trình bậc nhất, bậc hai

1. Phương trình chứa ẩn trong dấu giá trị tuyệt đối

Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta có thể dùng định nghĩa của giá trị tuyệt đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.

2. Phương trình chứa ẩn dưới dấu căn

Để giải phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một phương trình hệ quả không chứa ẩn dưới dấu căn.