Bài 2. Phương trình mặt phẳng
I. Vectơ pháp tuyến của mặt phẳng
Định nghĩa
Cho mặt phẳng $\left( \alpha \right)$. Nếu vectơ $\overrightarrow n \ne 0$ và có giá vuông góc với mặt phẳng $\left( \alpha \right)$ thì $\overrightarrow n $ được gọi là vectơ pháp tuyến của mặt phẳng $\alpha $. 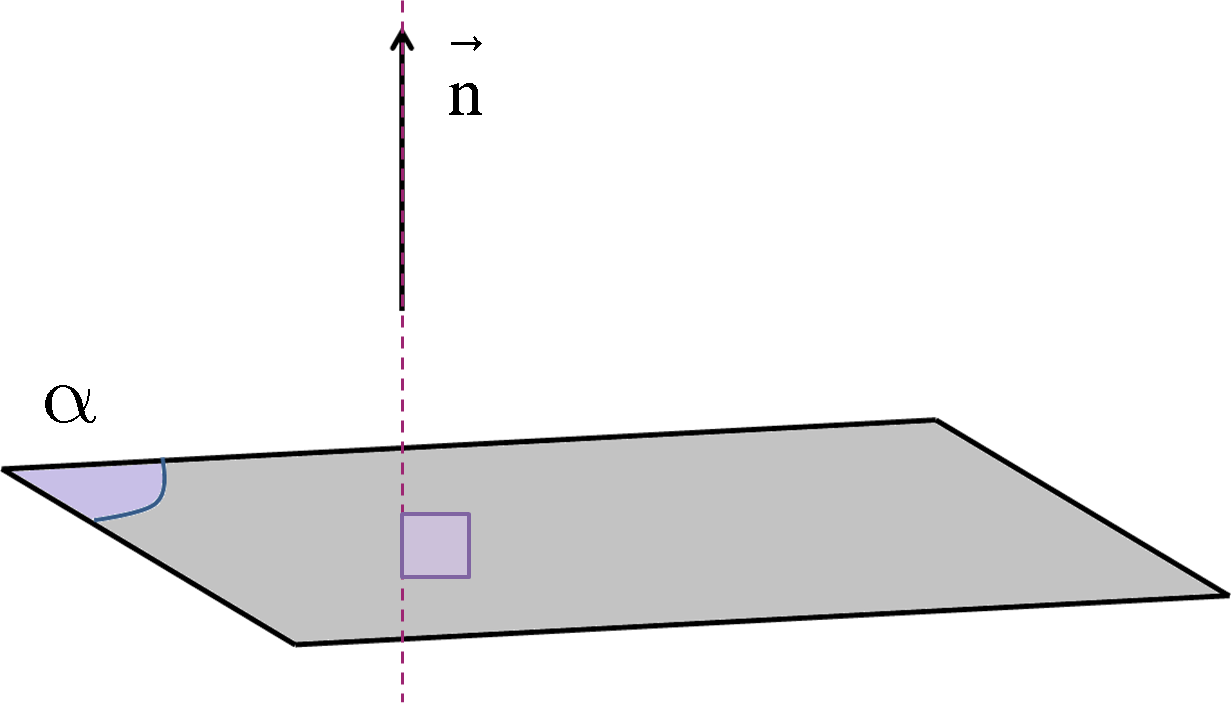
II. Phương trình tổng quát của mặt phẳng
1. Định nghĩa
Phương trình có dạng $Ax + By + Cz + D = 0$, trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng.
* Nhận xét:
a) Nếu mặt phẳng $\left( \alpha \right)$ có phương trình tổng quát là $Ax + By + Cz + D = 0$ thì nó có một vectơ pháp tuyến là $\overrightarrow n \left( {A;B;C} \right)$.
b) Phương trình mặt phẳng đi qua điểm ${M_o}\left( {{x_o};{y_o};{z_o}} \right)$ nhận vectơ $\overrightarrow n \left( {A;B;C} \right)$ làm vectơ pháp tuyến là $A\left( {x - {x_o}} \right) + B\left( {y - {y_o}} \right) + C\left( {z - {z_o}} \right) = 0$.
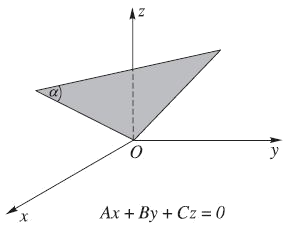
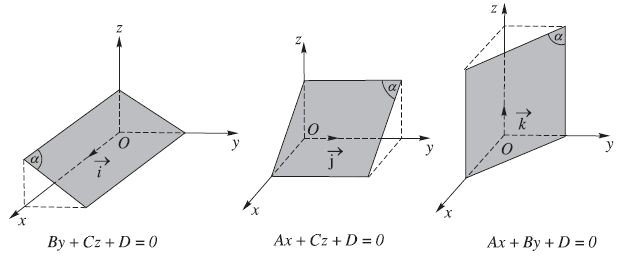
2. Các trường hợp riêng
Vị trí đặc biệt của mặt phẳng $\left( \alpha \right)$ so với trục tọa độ:
| Phương trình $\left( \alpha \right)$ | Đặc điểm của $\left( \alpha \right)$ |
|---|---|
| By + Cz + D = 0 | $\left( \alpha \right)$ song song hoặc chứa Ox |
| Ax+ Cz + D = 0 | $\left( \alpha \right)$ song song hoặc chứa Oy |
| Ax + By + D = 0 | $\left( \alpha \right)$ song song hoặc chứa Oz |
| Cz + D = 0 | $\left( \alpha \right)$ song song hoặc trùng với (Oxy) |
| By + D = 0 | $\left( \alpha \right)$ song song hoặc trùng với (Oxz) |
| Ax + D = 0 | $\left( \alpha \right)$ song song hoặc trùng với (Oyz) |

III. Điều kiện để hai mặt phẳng song song, vuông góc
1. Điều kiện để hai mặt phẳng song song
$\begin{array}{*{20}{l}}
\begin{array}{l}
\left( {{\alpha _1}} \right)//\left( {{\alpha _2}} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {{n_1}} = k\overrightarrow {{n_2}} }\\
{{D_1} \ne k{D_2}}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\left( {{A_1};{B_1};{C_1}} \right) = k\left( {{A_2};{B_2};{C_2}} \right)}\\
{{D_1} \ne k{D_2}}
\end{array}} \right.
\end{array}\\
\begin{array}{l}
\left( {{\alpha _1}} \right) \equiv \left( {{\alpha _2}} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {{n_1}} = k\overrightarrow {{n_2}} }\\
{{D_1} = k{D_2}}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\left( {{A_1};{B_1};{C_1}} \right) = k\left( {{A_2};{B_2};{C_2}} \right)}\\
{{D_1} = k{D_2}}
\end{array}} \right.
\end{array}
\end{array}$
2. Điều kiện để hai mặt phẳng vuông góc
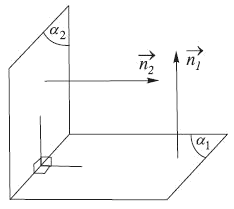
$\begin{array}{l}
\left(
{{\alpha _1}} \right) \bot \left( {{\alpha _2}} \right) \Leftrightarrow
\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\\
\Leftrightarrow {A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2} = 0
\end{array}$
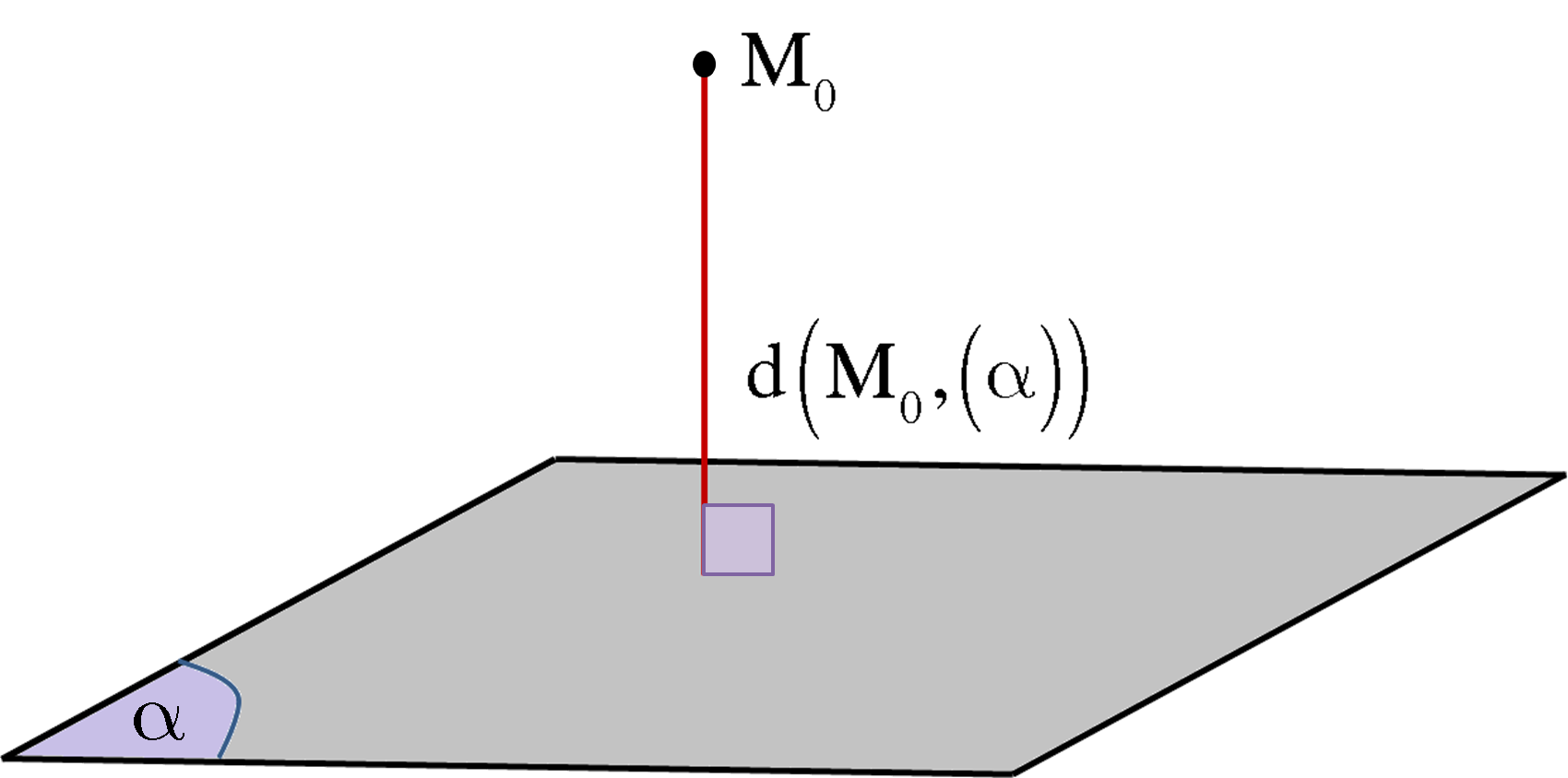
IV. Khoảng cách từ một điểm đến một mặt phẳng
Định lí:
Trong không gian Oxyz, cho mặt phẳng $\left( \alpha \right)$ có phương trình $Ax + By + Cz + D = 0$ và điểm ${M_o}\left( {{x_o};{y_o};{z_o}} \right)$. Khoảng cách từ điểm ${M_o}$ đến mặt phẳng $\left( \alpha \right)$, kí hiệu là $d\left( {{M_o},\left( \alpha \right)} \right)$, được tính theo công thức:
$d\left( {{M_o},\left( \alpha \right)} \right) = \frac{{\left| {A{x_o} + B{y_o} + C{z_o} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}$