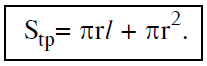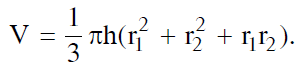1. Hình nón

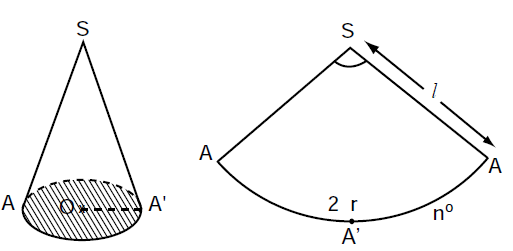
Khi quay một tam giác vuông góc $AOC$ một vòng quanh cạnh góc vuông $OA$ cố định thì được một hình nón.

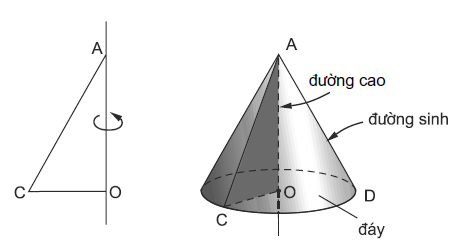
- Cạnh $OC$ tạo nên đáy của hình nón, là một hình nón tâm $O.$

- Cạnh $AC$ quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn $AD$ là một đường sinh.

- $A$ là đỉnh và $AO$ là đường cao của hình nón.

2. Diện tích xung quanh, diện tích toàn phần của hình nón

Công thức tính diện tích xung quanh của hình nón:

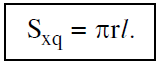
Công thức tính diện tích toàn phần của hình nón (tổng diện tích xung quanh và diện tích đáy):

Trong đó $r$ là bán kính đường tròn đáy, $l$ là đường sinh. 

3. Thể tích hình nón

Công thức tính thể tích hình nón:

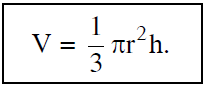
4. Hình nón cụt

Khi cắt hình nón bởi một mặt phẳng song song với thì phần mặt phẳng nằm trong hình nón là một hình tròn. Phần hình nón nằm giữa mặt phẳng nói trên với mặt đáy được gọi là một hình nón cụt.

5. Diện tích xung quanh và thể tích hình nón cụt

Cho hình nón cụt có $r_1,r_2$ là các bán kính đáy, $l$ là độ dài đường sinh, $h$ là chiều cao.

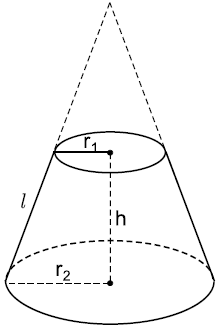
Công thức tính diện tích xung quanh nón cụt là:  

${S_{xq}} = \pi \left( {{r_1} + {r_2}} \right).l.$

Công thức tính thể tích nón cụt là: