Hàm số $y = {x^\alpha },\alpha  \in R$, được gọi là hàm số lũy thừa.

* Đạo hàm của hàm số lũy thừa

Một cách tổng quát, người ta chứng minh được hàm số lũy thừa $y = {x^\alpha },\alpha  \in R$ có đạo hàm với mọi x>0  và $\left( {{x^\alpha }} \right)' = \alpha {x^{\alpha  - 1}}$.

* Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa có dạng:

$\left( {{u^\alpha }} \right)' = \alpha {u^{\alpha  - 1}}.u'$

* Khảo sát hàm số lũy thừa $y = {x^\alpha }$

Tập xác định của hàm số lũy thừa $y = {x^\alpha }$ luôn chứa khoảng $\left( {0; + \infty } \right)$ với mọi $\alpha  \in R$. Trong trường hợp tổng quát, ta khảo sát hàm số $y = {x^\alpha }$ trên khoảng này (gọi là tập khảo sát).

1. $y = {x^\alpha },\alpha  > 0$

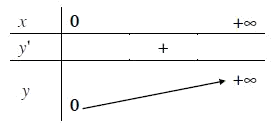
- Tập khảo sát: $\left( {0; + \infty } \right)$

- Sự biến thiên:
 $y' = \alpha {u^{\alpha  - 1}} > 0,\forall x > 0$

Giới hạn đặc biệt:
 $\mathop {\lim }\limits_{x \to {0^ + }} {x^\alpha } = 0,\mathop {\lim }\limits_{x \to  + \infty } {x^\alpha } =  + \infty $

Tiệm cận: không có.

- Bảng biến thiên:

- Đồ thị (Hình 5 với $\alpha  > 0$): 

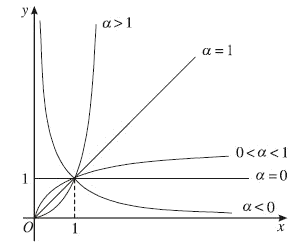
Hình 5

2. $y = {x^\alpha },\alpha  < 0$

- Tập khảo sát: $\left( {0; + \infty } \right)$

- Sự biến thiên:
 $y' = \alpha {u^{\alpha  - 1}} < 0,\forall x < 0$

Giới hạn đặc biệt:
 $\mathop {\lim }\limits_{x \to {0^ + }} {x^\alpha } =  + \infty ,\mathop {\lim }\limits_{x \to  + \infty } {x^\alpha } = 0$

Tiệm cận:

Trục Ox là tiệm cận ngang.

Trục Oy là tiệm cận đứng của đồ thị.  

- Bảng biến thiên:

- Đồ thị (Hình 5 với $\alpha  < 0$): 

Hình 5