Bài 2. Cực trị của hàm số
Cho hàm số $y = f\left( x \right)$ xác định và liên tục trên khoảng $\left( {a;b} \right)$ (có thể $a = - \infty ;b = + \infty $ và điểm ${x_o} \in \left( {a;b} \right)$.
- Nếu tồn tại h>0 sao cho $f\left( x \right) < f\left( {{x_o}} \right),\forall x \in \left( {{x_o} - h;{x_o} + h} \right),x \ne {x_o}$ thì ta nói hàm số $y = f\left( x \right)$ đạt cực đại tại ${x_o}$.
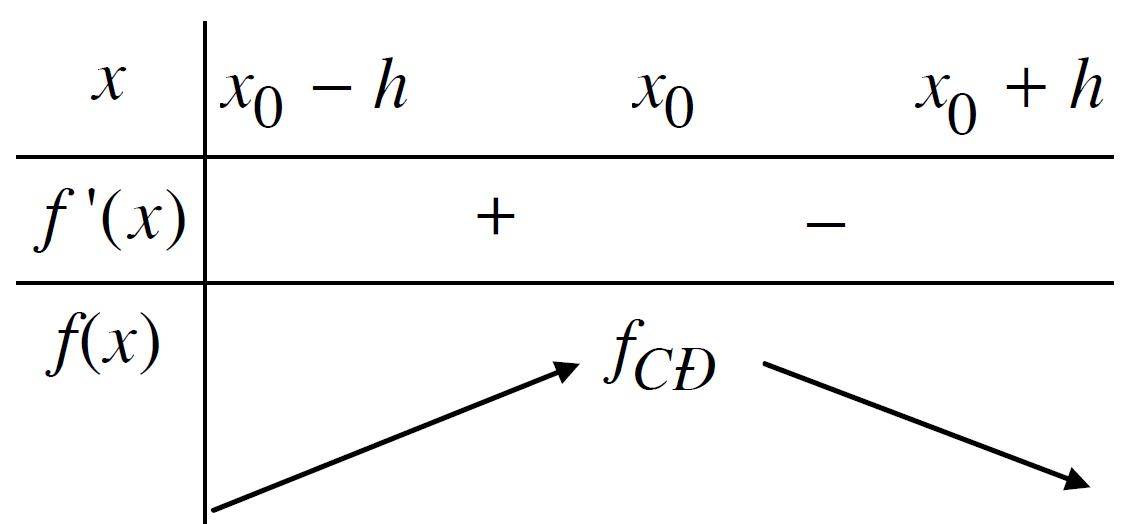
- Nếu tồn tại h>0 sao cho $f\left( x \right) > f\left( {{x_o}} \right),\forall x \in \left( {{x_o} - h;{x_o} + h} \right),x \ne {x_o}$ thì ta nói hàm số $y = f\left( x \right)$ đạt cực tiểu tại ${x_o}$.
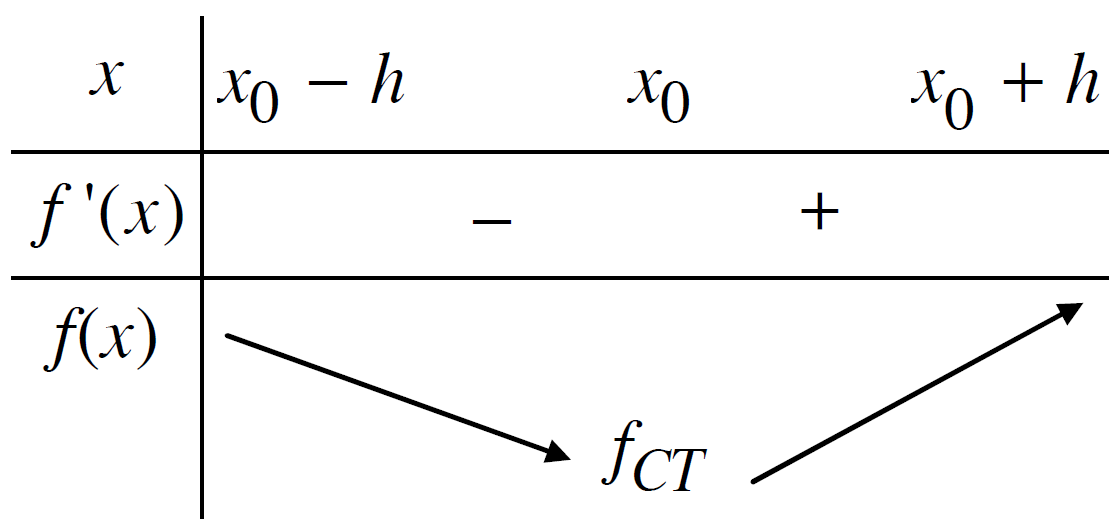
II. ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊ
* Định lí 1
Giả sử hàm số $y = f\left( x \right)$ liên tục trên khoảng $K = \left( {{x_0} - h;{x_0} + h} \right)$ và có đạo hàm trên K hoặc $K\backslash \left\{ {{x_0}} \right\}$, với h>0.
a) Nếu $f'\left( x \right) > 0$ trên khoảng $\left( {{x_0} - h;{x_0}} \right)$ và $f'\left( x \right) < 0$ trên khoảng $\left( {{x_0};{x_0} + h} \right)$ thì ${{x_0}}$ là một điểm cực đại của hàm số $f\left( x \right)$.
b) Nếu $f'\left( x \right) < 0$ trên khoảng $\left( {{x_0} - h;{x_0}} \right)$ và $f'\left( x \right) > 0$ trên khoảng $\left( {{x_0};{x_0} + h} \right)$ thì ${{x_0}}$ là một điểm cực tiểu của hàm số $f\left( x \right)$.
Ví dụ: Cho hàm số $y = \frac{1}{4}{x^3} - \frac{3}{2}{x^2} + 5.$
Ta có: $y' = \frac{3}{4}{x^2} - 3x.$
Bảng biến thiên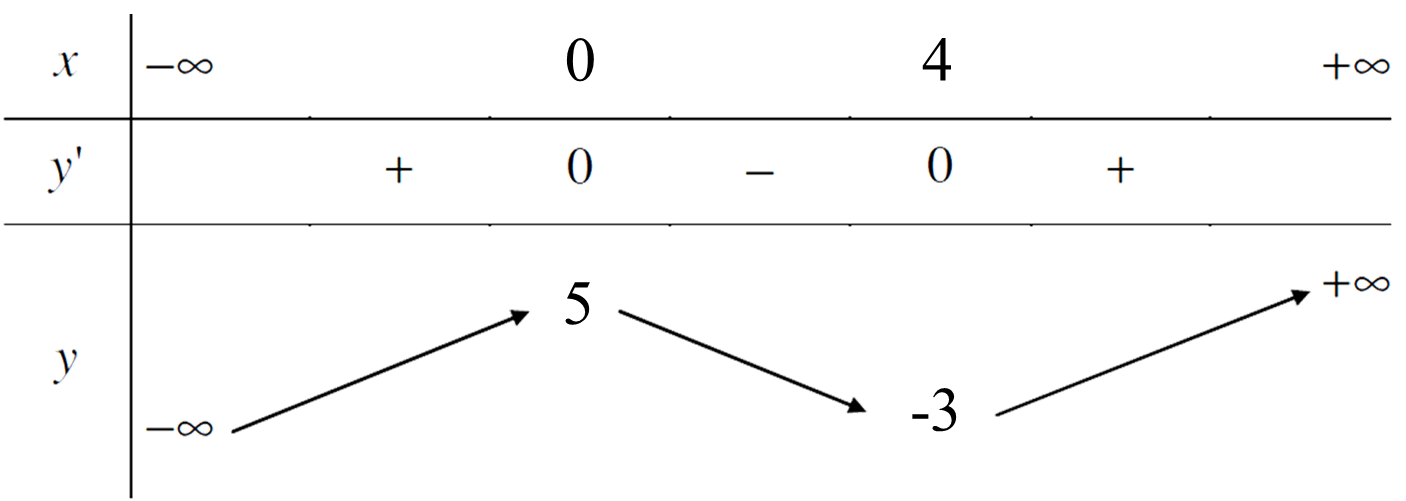
Đồ thị 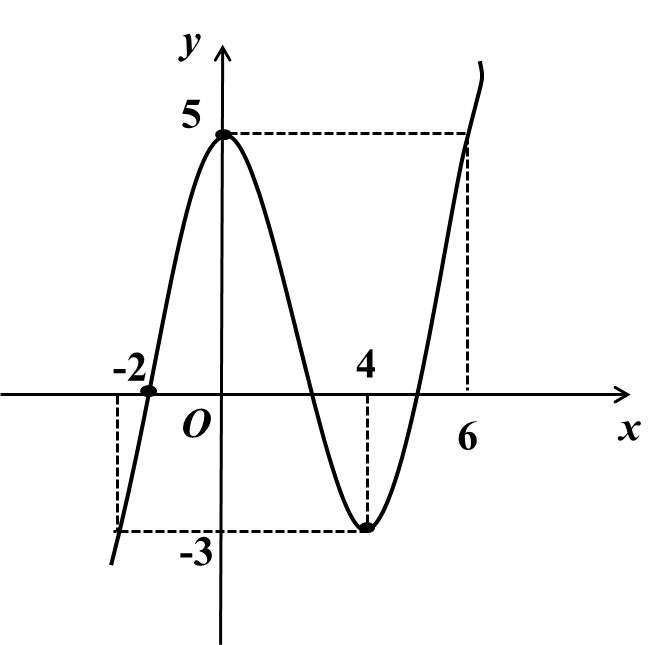
Vậy hàm số đã cho có tọa độ điểm cực đại là $\left( {0;5} \right)$ và cực tiểu là $\left( {4; - 3} \right).$
III. QUY TẮC TÌM CỰC TRỊ
Ta có các quy tắc tìm cực trị sau:
1. Quy tắc I:
- Tìm tập xác định.
- Tính $f'\left( x \right)$. Tìm các điểm tại đó $f'\left( x \right) = 0$ hoặc $f'\left( x \right)$ không xác định.
- Lập bảng biến thiên.
- Từ bảng biến thiên suy ra các điểm cực trị.
* Định lí 2
Giả sử hàm số $f\left( x \right)$ có đạo hàm cấp hai trong khoảng
$\left( {{x_0} - h;{x_0} + h} \right)$, với h > 0. Khi đó:
a) Nếu
$f'\left( {{x_0}} \right) = 0,f''\left( {{x_0}} \right) > 0$ thì
${x_0}$ là điểm cực tiểu;
b) Nếu
$f'\left( {{x_0}} \right) = 0,f''\left( {{x_0}} \right) < 0$ thì
${x_0}$ là điểm cực đại.
2. Quy tắc II:
- Tìm tập xác định.
- Tính $f'\left( x \right)$. Giải phương trình $f'\left( x \right) = 0$ và kí hiệu ${x_i}\left( {i = 1,2,...,n} \right)$ là các nghiệm của nó.
- Tính $f''\left( x \right);f''\left( {{x_i}} \right)$.
- Dựa vào dấu của $f''\left( {{x_i}} \right)$ suy ra tính chất cực trị của điểm ${x_i}$.
Ví dụ: Tìm cực trị của hàm số $f\left( x \right) = \frac{{{x^4}}}{4} - 2{x^2} + 6$Giải: Hàm số xác định với mọi $x \in R$
$\begin{array}{l}f'\left( x \right) = {x^3} - 4x = x\left( {{x^2} - 4} \right)\\f'\left( x \right) = 0 \Rightarrow {x_1} = - 2;{x_2} = 2.\\f''\left( x \right) = 3{x^2} - 4.\\f''\left( { \pm 2} \right) = 8 > 0\end{array}$
$ \Rightarrow x = - 2$ và $x = 2$ là hai điểm cực tiểu.
$f''\left( 0 \right) = - 4 < 0$
$ \Rightarrow x = 0$ là điểm cực đại.
Kết luận:
$f\left( x \right)$ đạt cực tiểu tại $x = - 2$ và $x = 2$; ${f_{CT}} = f\left( { \pm 2} \right) = 2$.
$f\left( x \right)$ đạt cực đại tại x = 0 và ${f_{CĐ}} = f\left( 0 \right) = 6$.



