1. Định nghĩa đường tròn

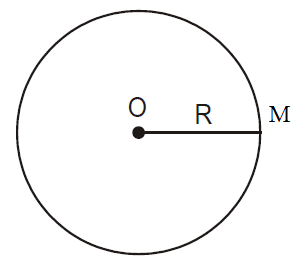
Đường tròn tâm $O$ bán kính $R,$ kí hiệu $(O;R),$ là hình gồm các điểm cách $O$ một khoảng bằng $R.$

Nếu $M$ nằm trên đường tròn $(O;R)$ thì $OM=R.$

Nếu $M$ nằm trong đường tròn $(O;R)$ thì $OM<R.$

Nếu $M$ nằm ngoài đường tròn $(O;R)$ thì $OM>R.$

2. Cách xác định đường tròn

- Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.

- Tâm $O$ của đường tròn đi qua ba điểm $A, B, C$ là giao điểm của ba đường trung trực của tam giác $ABC.$

3. Tâm đối xứng

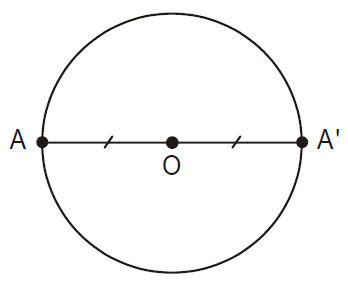
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.

4.Trục đối xứng

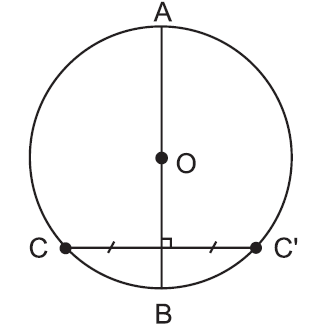
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.

Chú ý:

* Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.

* Trong tam giác đều, tâm đường tròn ngoại tiếp là trọng tâm tam giác đó.