1. Hàm số sin và hàm số côsin

a) Hàm số sin

Hàm số $y = \sin x$ có tập xác định R là $ - 1 \le \sin x \le 1,\forall x \in R$.

$y = \sin x$ là hàm số lẻ.

$y = \sin x$ là hàm số tuần hoàn với chu kì $2\pi $.

Hàm số $y = \sin x$ nhận các giá trị đặc biệt:

* $\sin x = 0$ khi $x = k\pi ,k \in Z$.

* $\sin x = 1$ khi $x = \frac{\pi }{2} + k2\pi ,k \in Z$.

* $\sin x =  - 1$ khi $x =  - \frac{\pi }{2} + k2\pi ,k \in Z$.

Đồ thị hàm số $y = \sin x$:

b) Hàm số côsin

Hàm số $y = \cos x$ có tập xác định R là $ - 1 \le \cos x \le 1,\forall x \in R$.

$y = \cos x$ là hàm số chẵn.

$y = \cos x$ là hàm số tuần hoàn với chu kì $2\pi $.

Hàm số $y = \cos x$ nhận các giá trị đặc biệt:

* $\cos x = 0$ khi $x = \frac{\pi }{2} + k\pi ,k \in Z$.

* $\cos x = 1$ khi $x = k2\pi ,k \in Z$.

* $\cos x =  - 1$ khi $x = \left( {2k + 1} \right)\pi ,k \in Z$.

Đồ thị hàm số $y = \cos x$: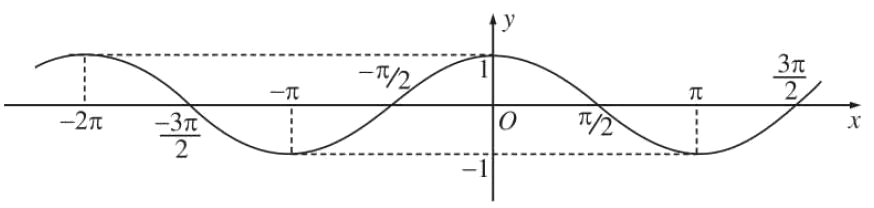

2. Hàm số tang và côtang

a) Hàm số tang

Hàm số $y = \tan x = \frac{{\sin x}}{{\cos x}}$ có tập xác định R là $D = R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}$.

$y = \tan x$ là hàm số lẻ.

$y = \tan x$ là hàm số tuần hoàn với chu kì $\pi $.

Hàm số $y = \tan x$ nhận các giá trị đặc biệt:

* $\tan x = 0$ khi $x = k\pi ,k \in Z$.

* $\tan x = 1$ khi $x = \frac{\pi }{4} + k\pi ,k \in Z$.

* $\tan x =  - 1$ khi $x =  - \frac{\pi }{4} + k\pi ,k \in Z$ .

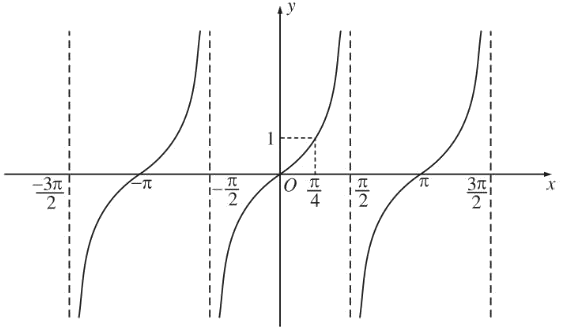
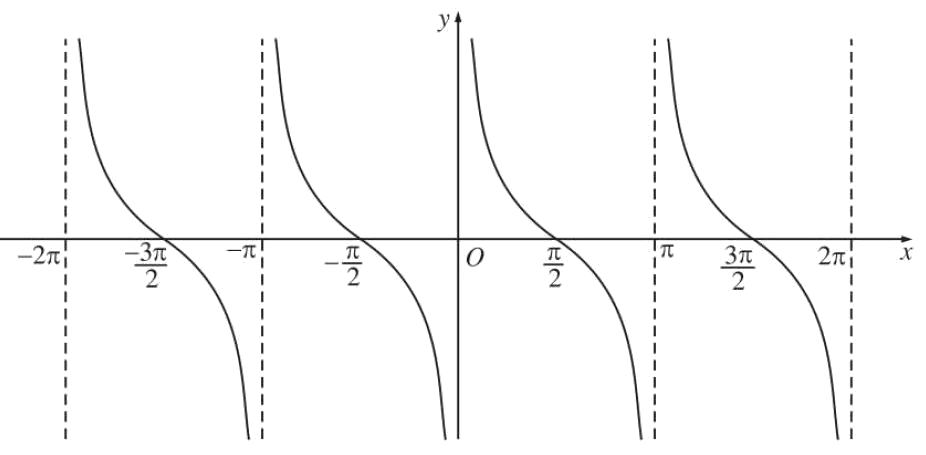
b) Hàm số côtang

Hàm số $y = \cot x = \frac{{\cos x}}{{\sin x}}$ có tập xác định R là $D = R\backslash \left\{ {k\pi ,k \in Z} \right\}$.

$y = \cot x$ là hàm số lẻ.

$y = \cot x$ là hàm số tuần hoàn với chu kì $\pi $.

Hàm số $y = \cot x$ nhận các giá trị đặc biệt:

* $\cot x = 0$ khi $x = \frac{\pi }{2} + k\pi ,k \in Z$.

* $\cot x = 1$ khi $x = \frac{\pi }{4} + k\pi ,k \in Z$.

Đồ thị hàm số $y = \cot x$: