I. Các tính chất thừa nhận

Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.

Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

Tính chất 3. Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng.

Tính chất 4. Có bốn điểm không cùng thuộc một mặt phẳng.

Tính chất 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.

Từ đó suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.

Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

II. Cách xác định mặt phẳng

Một mặt phẳng hoàn toàn được xác định khi biết:

1. Nó đi qua ba điểm không thẳng hàng;

2. Nó đi qua một điểm và chứa một đường thẳng đi qua điểm đó;

3. Nó chứa hai đường thẳng cắt nhau.

Kí hiệu:

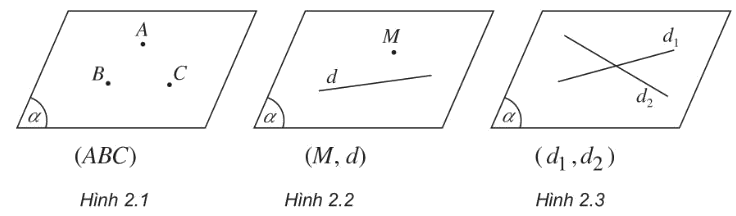
- (ABC) biểu thị mặt phẳng xác định bởi ba điểm phân biệt không thẳng hàng A, B, C. (Hình 2.1)

- (M,d) biểu thị mặt phẳng xác định bởi đường thẳng d và điểm M không nằm trên d. (Hình 2.2)

- (d₁,d₂) biểu thị mặt phẳng xác định bởi hai đường thẳng cắt nhau d₁,d₂. (Hình 2.3)

III. Hình chóp và hình tứ diện

1. Hình chóp

Trong mặt phẳng $\alpha $ cho đa giác lồi ${A_1}{A_2}...{A_n}$. Lấy điểm S nằm ngoài $\left( \alpha  \right)$. Lần lượt nối S với các đỉnh ${A_1}{A_2}...{A_n}$ ta được n tam giác $S{A_1}{A_2},S{A_2}{A_3},...S{A_n}{A_1}$. Hình gồm đa giác ${A_1}{A_2}...{A_n}$ và n tam giác $S{A_1}{A_2},S{A_2}{A_3},...S{A_n}{A_1}$ được gọi là hình chóp, kí hiệu là $S.{A_1}{A_2}...{A_n}$.

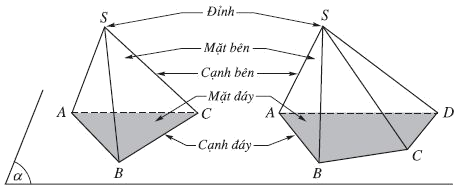
2. Hình tứ diện

Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ABD, ACD và BCD được gọi là hình tứ diện, kí hiệu là ABCD.