1. Hệ thức giữa đoạn nối tâm và bán kính

a) Hai đường tròn cắt nhau

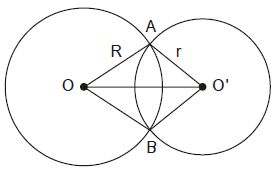
Trong hình trên, hai đường tròn $(O)$ và $(O’)$ cắt nhau tại $A$ và $B$.

Nếu $(O)$ và $(O’)$ cắt nhau thì $R-r<OO’<R+r.$

b) Hai đường tròn tiếp xúc nhau

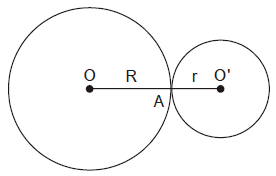
Trong hình trên, hai đường tròn $(O)$ và $(O’)$ tiếp xúc ngoài tại $A$, khi đó tiếp điểm $A$ nằm giữa $(O)$ và $(O’).$

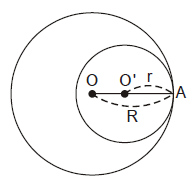
Trong hình trên, hai đường tròn $(O)$ và $(O’)$ tiếp xúc trong tại $A$, khi đó điểm $O’$ nằm giữa $(O)$ và $A.$

c) Hai đường tròn không giao nhau

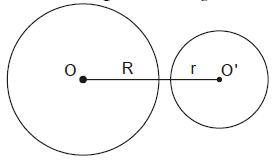
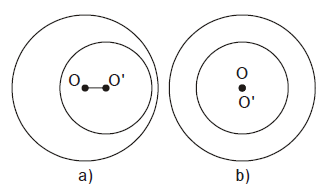
Trong hình trên, hai đường tròn $(O)$ và $(O’)$ không giao nhau và được gọi là hai đường tròn ở ngoài nhau.

Trong hình trên, hai đường tròn $(O)$ và $(O’)$ không giao nhau và đường tròn $(O)$ đựng đường $(O’)$. Trong trường hợp đặc biệt khi hai tâm trùng nhau (hình b) thì được gọi là hai đường tròn đồng tâm.

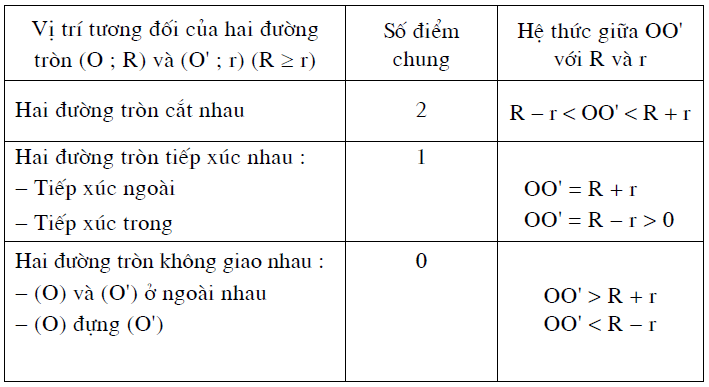
Ta có bảng sau:

2. Tiếp tuyến chung của hai đường tròn

Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.

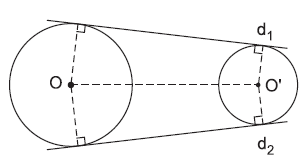
Trong hình trên, các đường thẳng $d_1$ và $d_2$ là các tiếp tuyến chung ngoài của hai đường tròn $(O)$ và $(O’)$ (tiếp tuyến chung ngoài không cắt đoạn nối tâm).

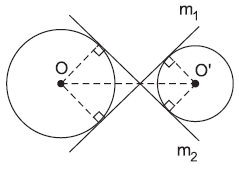
Trong hình trên, các đường thẳng $m_1$ và $m_2$ là các tiếp tuyến chung trong của hai đường tròn $(O)$ và $(O’)$ (tiếp tuyến chung trong cắt đoạn nối tâm).