7. Giao thoa sóng
I. Hiện tượng giao thoa của hai sóng mặt nước
Hiện tượng hai sóng gặp nhau tạo nên các gợn sóng ổn định gọi là hiện tượng giao thoa của hai sóng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa.
II. Cực đại và cực tiểu
1. Dao động của một điểm trong vùng giao thoa
Gọi M là một điểm trong vùng giao thoa. M cách S1,S2 những khoảng d1 và d2 gọi là đường đi của mỗi sóng tới M như hình vẽ.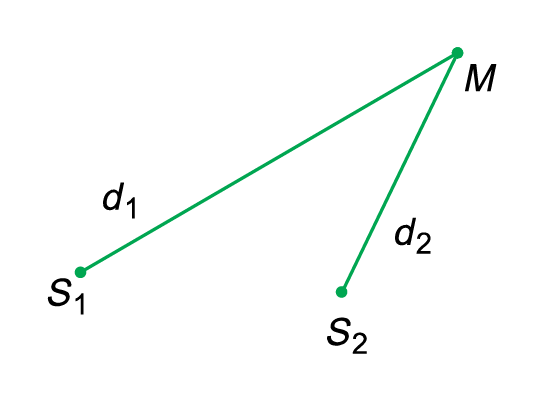
Chọn gốc thời gian sao cho phương trình dao động của hai nguồn là:
${u_{{S_1}}} = {u_{{S_2}}} = A\cos \frac{{2\pi t}}{T}$
Để cho đơn giản, ta coi biên độ của các sóng truyền tới M là bằng nhau và bằng biên độ của nguồn.
Vậy, dao động của phần tử tại M là dao động điều hòa cùng chu kì với hai nguồn và có biên độ dao động là:
${A_M} = 2A\left| {\cos \frac{{\pi ({d_2} - {d_1})}}{\lambda }} \right|$
Như vậy, tùy thuộc vào hiệu đường đi d2-d1 mà khi hai sóng đến gặp nhau tại M có thể luôn luôn tăng cường nhau làm cho phần tử tại M dao động mạnh lên, hoặc triệt tiêu nhau làm cho phần tử tại M đứng yên.
2. Vị trí cực đại và cực tiểu giao thoa
a) Vị trí các cực đại giao thoa
Cực đại giao thoa nằm tại các điểm có hiệu đường đi của hai sóng tới đó bằng một số nguyên lần bước sóng:
${d_2} - {d_1} = k\lambda$ ; (k=0,±1,±2,…)
Quỹ tích của những điểm này là những đường hypebol có hai tiêu điểm là S1 và S2 được gọi là những vân giao thoa cực đại.
b) Vị trí các cực tiểu giao thoa
Cực tiểu giao thoa nằm tại các điểm có hiệu đường đi của hai sóng tới đó bằng một số nửa nguyên lần bước sóng:
${d_2} - {d_1} = (k + \frac{1}{2})\lambda$ ; (k=0,±1,±2,…)
Quỹ tích của các điểm này là những đường hypebol mà hai tiêu điểm là S1 và S2 được gọi là những vân giao thoa cực tiểu.
III. Điều kiện giao thoa. Sóng kết hợp
Để có các vân giao thoa ổn định trên mặt nước thì hai nguồn sóng phải:
a) Dao động cùng phương, cùng chu kì (hay tần số).
b) Có hiệu số pha không đổi theo thời gian.
Hai nguồn như vậy gọi là hai nguồn kết hợp. Hai sóng do hai nguồn kết hợp phát ra gọi là hai sóng kết hợp.



