3. Con lắc đơn
I. Thế nào là con lắc đơn?
1. Định nghĩa
Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu của một sợi dây không dãn, khối lượng không đáng kể, dài l.
2. Vị trí cân bằng
Là vị trí mà dây treo có phương thẳng đứng.
Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc rồi thả ra, ta thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng thẳng đứng đi qua điểm treo và vị trí ban đầu của vật.
Ta hãy xét xem dao động của con lắc đơn có phải là dao động điều hòa hay không?
II. Khảo sát dao động của con lắc đơn về mặt động lực học
- Khảo sát dao động của con lắc đơn như hình vẽ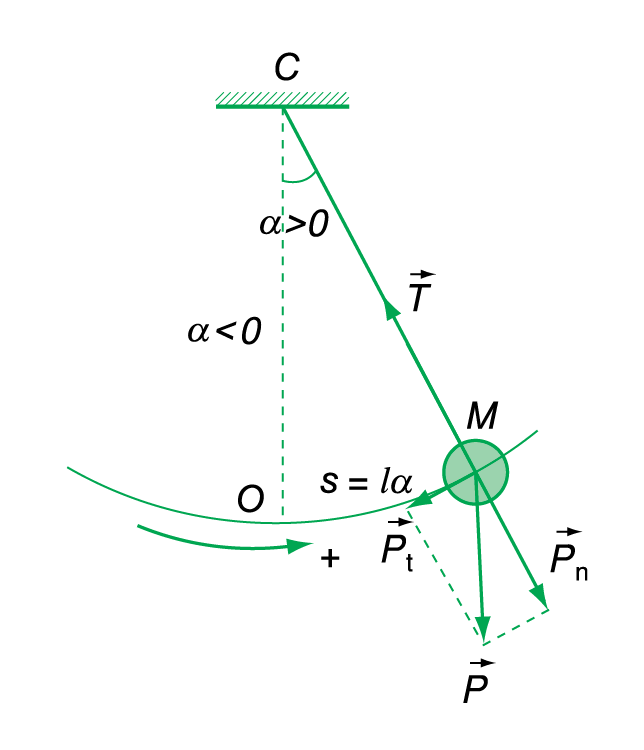
- Trong khi dao động, vật chịu tác dụng của trọng lực $\mathop P\limits^ \to $ và lực căng $\mathop T\limits^ \to $. Trọng lực $\mathop P\limits^ \to $ gồm $\mathop {{P_n}}\limits^ \to $ và $\mathop {{P_t}}\limits^ \to $.
Hợp lực của $\mathop T\limits^ \to $ và $\mathop {{P_n}}\limits^ \to $ là lực hướng tâm giữ cho vật chuyển động trên cung tròn.
Lực thành phần $\mathop {{P_t}}\limits^ \to $ là lực kéo về và có giá trị sau: Pt=-mgsinα.
Vậy dao động của con lắc đơn không phải là dao động điều hòa.
Nếu li độ góc α nhỏ thì sinα≈α (rad) nên lực kéo về Pt=-mgα= $mg\frac{s}{l}$.
Vậy, khi dao động nhỏ (sinα≈α (rad)), con lắc đơn dao động điều hòa theo phương trình: s=s0cos(ωt+φ).
Chu kì: $T = 2\pi.\sqrt {\frac{l}{g}} $ với s0 = lα0 là biên độ dao động.
III. Khảo sát dao động của con lắc đơn về mặt năng lượng
1. Động năng của con lắc đơn:
${W_đ} = \frac{1}{2}m{v^2}$
2. Thế năng của con lắc đơn ở li độ góc α:
${W_t} = mgl(1 - \cos \alpha )$ (mốc tính thế năng ở vị trí cân bằng)
3. Cơ năng của con lắc đơn:
Cơ năng của con lắc đơn được bảo toàn nếu bỏ qua mọi ma sát:
${W_{}} = \frac{1}{2}m{v^2} + mgl(1 - \cos \alpha )$
= hằng số
IV. Ứng dụng: xác định gia tốc rơi tự do
Đo gia tốc trọng trường trong lĩnh vực địa chất.



